Introdução
Nos últimos artigos, vimos o funcionamento das portas lógicas e aprendemos a usar a Álgebra Booleana para descrever e analisar circuitos gerados por meio da combinação de portas lógicas.
Esses circuitos são chamados de combinacionais, pois – em qualquer instante de tempo – o nível lógico da saída do circuito depende da combinação dos níveis lógicos das entradas.
Neste artigo vamos entender como implementar os circuitos combinacionais.
Desenvolvimento
Projetando Circuitos Lógicos Combinacionais
Primeiramente é preciso destacar que um circuito combinacional não conta com a característica de memória, logo sua saída depende apenas dos valores atuais das entradas.
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
A tabela verdade é o recurso que utilizamos para verificar o nível de saída de um circuito lógico para todas as condições de entrada possíveis. E por meio dessa tabela podemos obter a expressão booleana que viabiliza a construção do circuito.
Por exemplo, considerando a Tabela 1 vemos que x = 1 somente quando A = 0 e B = 1.
| A | B | x |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
A partir da tabela podemos concluir que a expressão que define saída é x=AB.
Isso acontece, pois ao analisar a tabela verdade vemos que a saída será 1 para apenas uma única combinação de entradas, o que caracteriza uma porta AND. Como a operação lógica AND somente permite que a saída seja 1 quando as duas entradas forem 1 e nós temos que A=0, então é preciso negar o A, ou seja, /A.
Observe que, com essa expressão, para todos os demais valores de A e B, a saída x será 0.
O circuito gerado é o mostrado na Figura 1, uma combinação das portas AND e NOT.
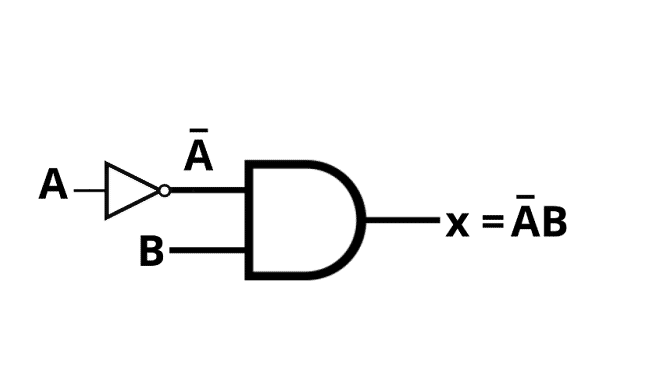
Para outras condições pode-se visualizar esse problema se comportar da mesma forma. Por exemplo, se x = 1 apenas para a condição A = 1 e B = 0, o circuito resultante seria uma porta AND com entradas A e /B. Isso significa que pode-se gerar uma saída 1 com qualquer uma das 4 combinações possíveis de entrada. Os 4 casos diferentes podem ser vistos na Figura 2.
Assim observamos que cada porta AND, da Figura 2, gera uma saída nível 1 somente para a condição de entrada dada e para todas as outras condições teremos 0 na saída.
Agora vamos considerar outro caso, mostrado na Tabela 2.
| A | B | x |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Aqui temos uma tabela-verdade que indica que a saída x será 1 para dois casos diferentes: se A = 0 e B = 1 ou A = 1 e B = 0. A implementação é simples: nós temos duas condições para ter uma saída 1, se x= /A B ou se x= A /B. Ou seja, x será 1 se atender mais de uma combinação de entradas diferentes. Isso significa que estamos trabalhando com uma porta OU.
Logo, a expressão booleana que representa esse circuito é x=AB + AB. Essa implementação é mostrada na Figura 3.
Note que no final as saídas de cada porta AND foram usadas como entrada para a porta OR, e é somente na saída da porta OR que teremos o nível lógico de x.
Procedimento Completo Para o Projeto de Circuitos Combinacionais
Qualquer problema lógico pode ser resolvido, com o seguinte processo:
1. Interpretação do problema e construção de uma tabela verdade para descrever seu funcionamento;
2. Para cada caso em que a saída seja 1 escreva as entradas em forma de AND (produto);
3. Se houver mais de uma combinação de entrada, escreva a expressão da soma de produtos para a saída;
4. Se possível simplifique a expressão de saída;
5. Com a expressão simplificada, implemente com os CIs adequados.
Referências
TOCCI, R.; WIDMER, N.; MOSS, G. Sistemas Digitais – Princípios e Aplicações. [S.l.]: Pearson Education Limited, 2011.
