Os sistemas de numeração são usados para representar a quantidade de determinados elementos. O sistemas mais usado pelas pessoas é o decimal. Esse sistema é formado por 10 algarismos. Para a eletrônica digital e sistemas de computação os sistemas binário, hexadecimal e octal são muito utilizados.
Entender as diferentes formas de representação numérica é muito importante para se trabalhar com eletrônica e programação. A seguir apresentaremos os detalhes de cada um desses sistemas de numeração mencionados.
Sistema de numeração decimal
O sistema de numeração decimal utiliza 10 algarismos para sua representação: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
Para formar um número, associa-se um ou mais algarismos, e a posição de cada algarismo terá um peso de uma potência de 10. Dessa forma temos as unidades, dezenas, centenas e milhares. Cada posição terá um peso na representação:
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
Como exibido na figura acima, o sistema decimal é representado na base 10 e cada posição é múltiplo de uma potência de 10. A seguir são apresentados alguns exemplos:
Número 523:
|
5 |
2 |
3 |
|
Centena |
dezena |
unidade |
|
5 x 102 |
2 x 101 |
3 x 100 |
|
500 |
20 |
3 |
|
500+20+3 = 523 |
Número 8079:
|
8 |
0 |
7 |
9 |
|
milhar |
Centena |
dezena |
unidade |
|
8 x 103 |
0 x 102 |
7 x 101 |
9 x 100 |
|
8000 |
0 |
70 |
9 |
|
8000+0+70+9 = 8079 |
Sistema de numeração Hexadecimal
O sistema de numeração hexadecimal utiliza 16 algarismos para sua representação: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F. Assim como no sistema decimal, a associação dos algarismos representam diferentes números e a posição do algarismos será um múltiplo de potência de 16. Assim, o sistema hexadecimal é um sistema de base 16. Podemos fazer uma relação entre o sistema hexadecimal e o sistema decimal, como exibido na tabela abaixo:
|
Decimal |
Hexadecimal |
|
0 |
0 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
8 |
|
9 |
9 |
|
10 |
A |
|
11 |
B |
|
12 |
C |
|
13 |
D |
|
14 |
E |
|
15 |
F |
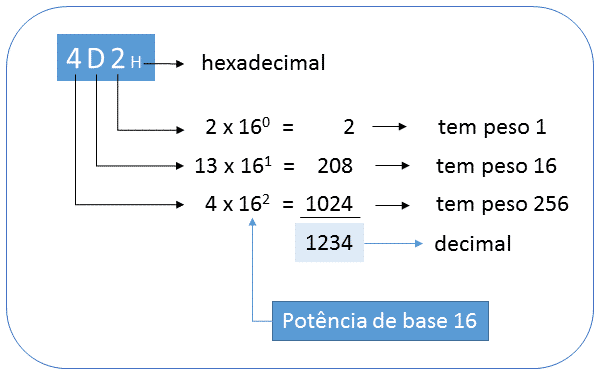
A seguir é exibida a representação de um número hexadecimal:
Como exibido figura acima, o sistema hexadecimal é representado na base 16 e cada posição é múltiplo de uma potência de 16. A seguir são apresentados alguns exemplos:
Número 1FH:
|
1 |
F |
|
1 X 161 |
15 X 160 |
|
16 |
15 |
|
16 + 15 = 31 decimal |
Número ABCH:
|
A |
B |
C |
|
10 x 162 |
11 X 161 |
12 X 160 |
|
2560 |
176 |
12 |
|
2560 + 176 + 12 = 2748 decimal |
Sistema de numeração Octal
O sistema de numeração octal utiliza 8 algarismos para sua representação: 0, 1, 2, 3, 4, 5, 6 e 7. Assim, o sistema octal possui base 8. A seguir é apresentada a representação de um número octal:
Como exibida figura acima, o sistema octal é representado na base 8 e cada posição é múltiplo de uma potência de 8. A seguir são apresentados alguns exemplos:
Número 1238:
|
1 |
2 |
3 |
|
1 x 82 |
2 X 81 |
3 X 80 |
|
64 |
16 |
3 |
|
64 + 16 + 3 = 83 decimal |
Número 108:
|
1 |
0 |
|
1 X 81 |
0 X 80 |
|
8 |
0 |
|
8 + 0 = 8 decimal |
Sistema de numeração binário
O sistema de numeração binário utiliza apenas dois algarismos para sua representação: 0 e 1. Assim é um sistema de base 2. Ele é muito usado para representação de valores em sistemas digitais. O seu conhecimento é muito importante para a área de eletrônica. A seguir é apresentada sua representação:
Como exibido figura acima, o sistema binário é representado na base 2 e cada posição é múltiplo de uma potência de 2. A seguir são apresentados alguns exemplos:
Número 102:
|
1 |
0 |
|
1 X 21 |
0 X 20 |
|
2 |
0 |
|
2 + 0 = 2 decimal |
Número 10102:
|
1 |
0 |
1 |
0 |
|
1 X 23 |
0 X 22 |
1 X 21 |
0 X 20 |
|
8 |
0 |
2 |
0 |
|
8+0+2 + 0 = 10 decimal |
Número 111111112:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 X 27 |
1 X 26 |
1 X 25 |
1 X 24 |
1 X 23 |
1 X 22 |
1 X 21 |
1 X 20 |
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
128+64+32+16+8+4+2+1 = 255 decimal |
Resumo das equivalências entre os sistemas de numeração decimal, hexadecimal, octal e binário
|
Decimal |
Hexadecimal |
Octal |
Binário |
|
0 |
0 |
0 |
0000 |
|
1 |
1 |
1 |
0001 |
|
2 |
2 |
2 |
0010 |
|
3 |
3 |
3 |
0011 |
|
4 |
4 |
4 |
0100 |
|
5 |
5 |
5 |
0101 |
|
6 |
6 |
6 |
0110 |
|
7 |
7 |
7 |
0111 |
|
8 |
8 |
10 |
1000 |
|
9 |
9 |
11 |
1001 |
|
10 |
A |
12 |
1010 |
|
11 |
B |
13 |
1011 |
|
12 |
C |
14 |
1100 |
|
13 |
D |
15 |
1101 |
|
14 |
E |
16 |
1110 |
|
15 |
F |
17 |
1111 |
Chegamos ao fim deste artigo. Acima foram apresentados os sistemas de numeração utilizados em eletrônica e programação, assim como alguns exemplos. No próximo artigo trataremos das conversões entre as bases.
Se ficou alguma dúvida, por favor deixe seu comentário.
Muito bom artigo, deu para refrescar a memória. Parabéns!
Otima explicação.
otima explicação