Circuito RC: Carga e descarga de capacitores

Agora que já conhecemos o funcionamento individual dos resistores e capacitores, podemos estudar um circuito muito útil formado por um resistor e um capacitor.

Estes circuitos são denominados circuitos RC e, embora sejam simples, possuem inúmeras aplicações em eletrônica, comunicações e sistemas de controle. 

A análise de circuitos RC é feita aplicando as leis de Kirchhoff tal qual foi feito para os circuitos resistivos. A principal diferença é que a aplicação das leis de Kirchhoff a circuitos resistivos resulta em equações algébricas, já a aplicação dessas leis a circuitos RC produz equações diferenciais de primeira ordem, que são mais difíceis de resolver do que as algébricas. 

Neste artigo vamos analisar o comportamento da saída para circuito sem fonte e com uma entrada degrau.

Circuitos RC sem fonte

Um circuito RC sem fonte ocorre quando sua fonte de corrente contínua é desconectada abruptamente. Assim, a energia armazenada no capacitor é liberada para os resistores. Para entender o funcionamento desse circuito, vamos considerar o circuito mostrado na Figura 1.

    O objetivo da análise é determinar a resposta do circuito, que nesse caso é a tensão v(t) no capacitor. Como o capacitor está inicialmente carregado, pode-se supor que no instante t = 0 a tensão inicial seja é V₀.

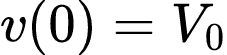
    E a energia armazenado no instante 0 é dada por:

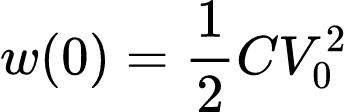
    Ao aplicar LKC ao nó superior, temos que a corrente é:

    Por definição, temos:

    Logo:

    A equação encontrada trata-se de uma equação diferencial de primeira ordem. Isso porque, há somente a primeira derivada de V envolvida. Para encontrar o V isolado, primeiramente será preciso fazer a seguinte manipulação algébrica.

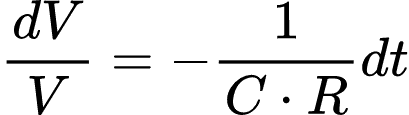
    A razão para isso é facilitar a integração em ambos os lados necessária para isolar V. Assim, após integrar, temos:

    Onde ln A é a constante de integração. Usando as propriedades logarítmicas, temos:

    Finalmente, é possível isolar v:

    Lembrando das condições iniciais, temos que v(0) = A = V_o. Logo:

    O resultado encontrado é que a resposta em tensão do circuito RC é uma queda exponencial da tensão inicial. Essa resposta se deve tanto à energia inicial armazenada, quanto às características físicas do circuito.

Como esse desempenho não é gerado por alguma fonte de tensão ou de corrente externa, ela é chamada de resposta natural do circuito.

    Graficamente fica mais fácil visualizar esse comportamento. Observe na Figura 2, que quando t = 0 temos a condição inicial V₀. Na medida em que se aumenta o t, a tensão vai diminuindo, cada vez mais se aproximando de 0. 

    A velocidade em que a tensão diminui é expressa em termos da constante de tempo, representada por τ (tau). 

A constante de tempo de um circuito é o tempo necessário para que a tensão diminua 36,8% ( 1/e) de seu valor inicial.

    Logo, quando t = τ, temos:

    Isso implica que τ = RC, portanto:

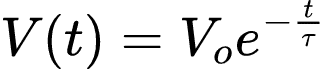
Em resumo, para se trabalhar com um circuito RC sem fonte é necessário determinar:

1. A tensão inicial v(0) = V_o no capacitor
   • Em posse da tensão do capacitor torna-se possível determinar outros valores, como: a corrente de capacitor i_C, a tensão v_R e a corrente do resistor i_R.
2. A constante de tempo τ

Exemplo RC sem fonte

   Para entender como trabalhar com circuitos RC, façamos um exemplo. Considere o circuito da Figura 3, com V_c(0)= 15 V, para determinar V_c, V_x e i_x para t > 0.

O primeiro passo para resolver o problema é adequar o circuito da Figura 3 ao circuito RC padrão, como mostrado na Figura 4. Assim, determinamos a resistência equivalente ou a resistência de Thévenin nos terminais do capacitor.

Então, os resistores de 8 Ω e 12 Ω em série serão associados, resultando em um resistor de 20 Ω. Por sua vez a resistência de 20 Ω está em paralelo com o resistor de 5 Ω, associando ambos temos uma resistência equivalente:

Nosso objetivo sempre é obter, primeiramente, a tensão V_C no capacitor. E através desta, determinar V_x e i_x. Assim, com o R_eq é possível determinar a constante do tempo.

    Logo:

    Ou seja:

Utilizando o princípio da divisão de tensão para obter V_x, temos:

Por último, encontramos que i_x é:

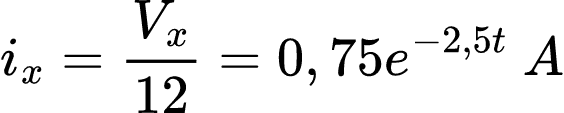
Resposta a um degrau de um circuito RC

Agora vamos entender o comportamento do circuito quando submetido a fonte de tensão ou de corrente modelada como uma função degrau. A resposta para esse tipo de entrada é conhecida como resposta a um degrau.

A resposta a um degrau é a resposta do circuito decorrente de uma aplicação repentina de uma fonte de tensão ou de corrente CC (corrente contínua). 

    Para entender esse comportamento, vamos considerar o circuito RC da Figura 5.

Da mesma forma, a tensão do capacitor será a resposta do circuito. Iremos supor, também, uma tensão inicial V₀ no capacitor, apesar de que isso não é necessário para a resposta a um degrau. Isso porque a tensão de um capacitor não muda instantaneamente:

    Chamamos de v(0^–) a tensão no capacitor imediatamente antes da chave fechar e v(0⁺) a tensão imediatamente após a fechar a chave. 

Aplicando a LKC, obtemos:

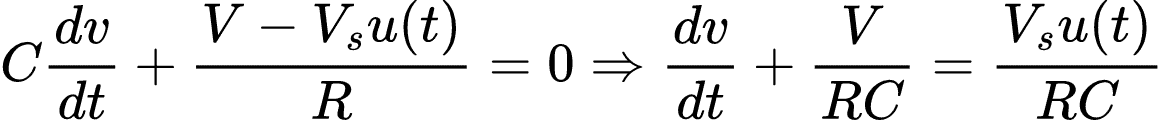
    Lembrando que v é a tensão no capacitor. Para t > 0, a equação ficará:

    Rearranjando os termos, temos:

    Ao integrar os dois lados, considerando as condições iniciais, obtemos:

    Logo, a resposta ao degrau é:

Essa expressão é conhecida como resposta completa, ou resposta total, de um circuito RC à aplicação repentina de uma fonte de tensão CC. 

Considerando que o capacitor esteja inicialmente carregado e assumindo V_s>V₀, temos o comportamento mostrado no gráfico da Figura 6.

    Mas se considerarmos que o capacitor está inicialmente descarregado, temos que V₀ = 0, logo a equação terá o seguinte formato:

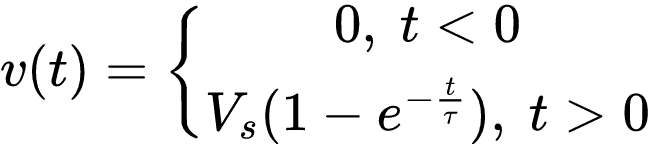
    Podemos ser resumido somente a:

    A equação encontrada descreve a resposta completa a um degrau do circuito RC quando o capacitor está inicialmente descarregado. 

Para obter a corrente através do capacitor utiliza-se a equação encontrada usando i(t) = C ‧ dv/dt. Assim, obtemos:

    Logo, a corrente sobre o capacitor é:

    O comportamento para esse caso é o mostrado no gráfico da Figura 7.

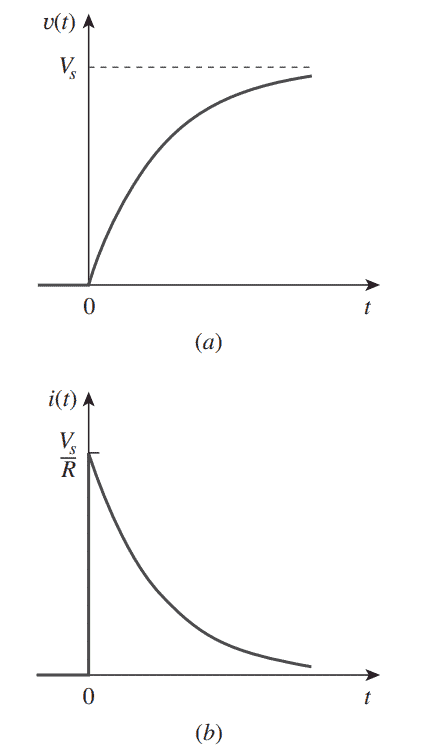
    Uma forma de evitar as derivadas é utilizar um método simplificado para determinar a resposta a um degrau de um circuito RC. Ao analisar a equação abaixo (que foi desenvolvida ao longo do texto)

É possível notar que v(t) possui duas componentes, nesse sentido, existem duas maneiras de decompô-la em duas componentes. 

A primeira delas é dividi-la em resposta natural e resposta forçada, de forma que:

Ou seja,

A resposta natural (v_n) do circuito diz respeito ao comportamento do próprio circuito, sem a presença de fonte externa de excitação. Já a resposta forçada (v_f), diz respeito à quando um agente externo (uma fonte de tensão ou corrente) é aplicado.

Outra maneira de se avaliar a resposta completa é dividi-la em duas componentes: temporária e permanente, isto é:

Ou seja,

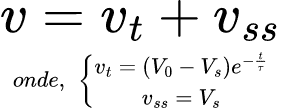
    A resposta transiente é a resposta temporária do circuito que se consome com o tempo. Enquanto a resposta em regime estacionário é a forma que o circuito se comporta um longo tempo após a excitação externa ter sido aplicada.

Em resumo, para encontrar a resposta a um degrau de um circuito RC é necessário determinar:

1. A tensão inicial v(0) do capacitor
   1. Em posse da tensão do capacitor torna-se possível determinar outros valores, como: a corrente de capacitor i_C, a tensão v_R e a corrente do resistor i_R.
2. A tensão final v() no capacitor
3. A constante de tempo τ

Referências

ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.