Em algumas situações é necessário medir a eficácia de uma fonte de tensão (ou de corrente) ao liberar potência para uma carga resistiva. Esse conceito é chamado de valor eficaz ou RMS.
Normalmente, quando se fala de tensões ou correntes senoidais normalmente expressamos em termos de seu valor máximo, ou do valor RMS. Por exemplo, o setor de energia elétrica especifica os 110 V ou 220 V em termos dos valores RMS. Analogamente, tanto os voltímetros quanto os amperímetros analógicos são projetados para exibir o valor RMS da tensão e da corrente, respectivamente.
Por isso, é importante saber expressar tensão e corrente em seus valores RMS e neste artigo veremos como determinar a corrente e a tensão eficaz (ou RMS).
Como calcular o valor RMS ou Eficaz
Na Figura 1a temos um circuito CA, já na Figura 1b o circuito é CC. Para entender corrente e tensão eficaz vamos determinar a Ief que será capaz de transferir a mesma potência ao resistor R como a senoide i(t).
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
Lembrando que a potência média absorvida pelo resistor no circuito CA é:
Já a potência absorvida pelo resistor no circuito CC é:
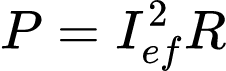
Igualando as duas equações, teremos que Ief, será:
De maneira análoga, o valor eficaz da tensão é obtido:
Isso significa que o valor eficaz é a raiz quadrada da média do quadrado da senoide. Por essa razão, o valor eficaz é conhecido como raiz do valor médio quadrático (Root-Mean-Square), ou seja, valor RMS. Portanto, escrevemos a corrente e tensão como:
Dessa forma, é possível generalizar que para qualquer função periódica x(t), o valor RMS é:
Como o valor eficaz é a raiz do valor médio quadrático, o valor RMS de uma constante é a própria constante. Para uma senóide x(t) = xmcos(ωt), o valor RMS é:
Ou seja, para i(t) e v(t) temos:
Lembrando que essas equações somente são válidas para sinais senoidais.
Obtido o valor RMS, a potência média pode ser reescrita como:
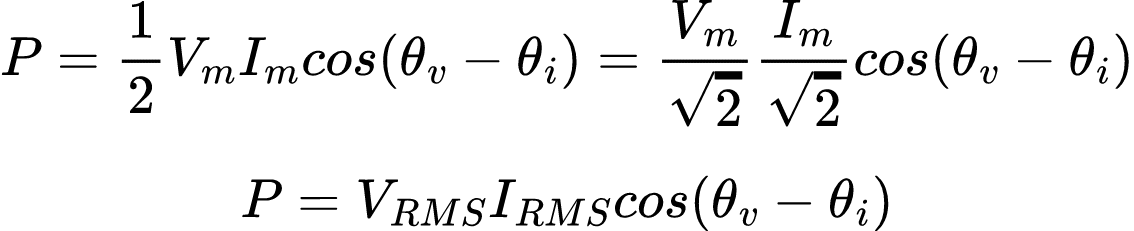
De maneira análoga, a potência média absorvida por um resistor R será reescrita como:
Exemplo
Para entender o valor RMS, vamos determiná-lo através da forma de onda mostrada na Figura 2.
Fonte: ALEXANDER (2013).
Observando a forma de onda, temos que o período T é 4. Ao longo de um período, é possível perceber que a forma de onda da corrente se comporta da seguinte forma:
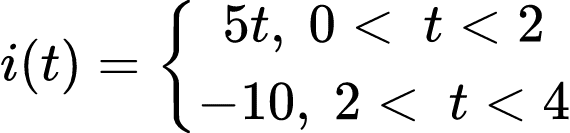
Então, o valor de IRMS é:
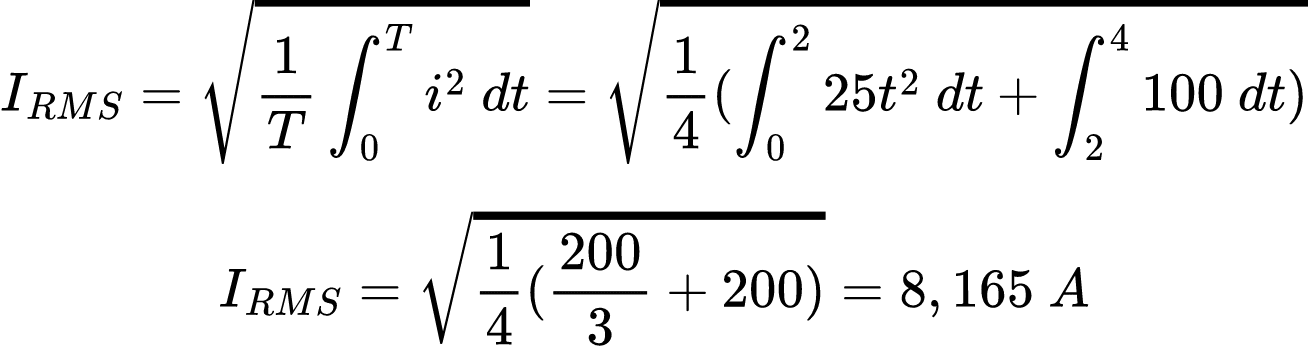
Se essa corrente passa através de um resistor de 2 Ω, a potência média absorvida pelo resistor é:
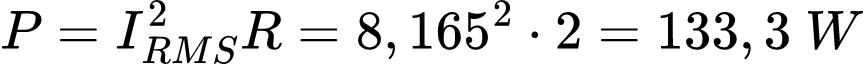
Referência
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
Muito bom. Parabéns. 🙂