Triângulo das potências e fator de potência

Neste artigo entenderemos os últimos conceitos de potência, triângulo das potências e fator de potência, úteis para analisar os circuitos CA.

Potência Aparente e Fator de Potência

Lembrando o artigo de Potência em CA, se a tensão e a corrente nos terminais de um circuito forem uma senoide com esse formato:

A potência média será:

Do artigo de Valor RMS, vimos que a potência média pode ser reescrita como:

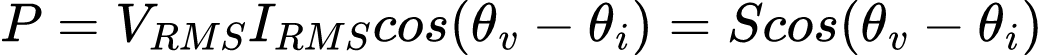
Mas agora temos um novo termo na equação

Agora vamos visualizar a potência média como produto de dois termos, com nomenclatura própria. O produto V_RMS‧I_RMS é chamado de potência aparente S, enquanto cos(θ_v – θ_i) é nomeado fator de potência (FP).

A potência aparente é medida em volt-ampères (VA) para distingui-la da potência média ou real medidas em Watts. Já o fator de potência é adimensional, já que é a razão entre a potência média e a potência aparente:

O ângulo θ_v – θ_i é conhecido como ângulo do fator de potência, afinal ele é o ângulo cujo cosseno é o fator de potência. Esse ângulo é o mesmo ângulo da impedância da carga, se V for a tensão na carga e I a corrente que passa por ela. Isso pode ser provado através de:

Lembrando que quando o símbolo está em negrito estamos fazendo referência a um fasor. Pegando V_RMS e I_RMS fasorial, temos:

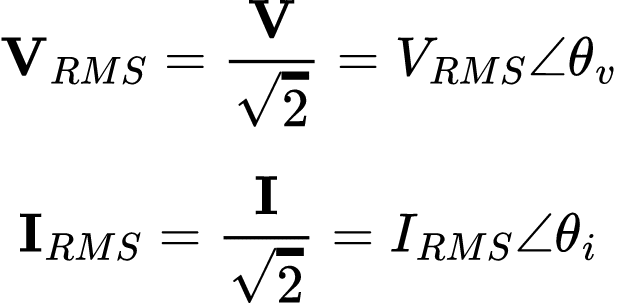
Então, a impedância é:

Logo:

O fator de potência, além de ser o cosseno da diferença de fase da tensão e da corrente, também é o cosseno do ângulo da impedância da carga.

O fator de potência também pode ser visto como o elemento em que a potência aparente deve ser multiplicada para se obter a potência média ou real. E seu valor varia entre 0 e 1. 

Assim, nós temos dois casos especiais:

• Para uma carga puramente resistiva, a tensão e a corrente estão em fase, então θ_v – θ_i= 0, ou seja, FP = 1. Nesse caso, a potência aparente será igual à potência média. 
• Para uma carga puramente reativa, θ_v – θ_i = 90°, ou seja, FP = 0. Nessa situação, a potência média é zero. 

Nesses dois casos, é dito que o fator de potência está adiantado ou atrasado. Um FP adiantado é aquele em que a corrente está à frente da tensão, o que indica uma carga capacitiva. Já o FP atrasado implica que a corrente está atrasada em relação à tensão, indicando uma carga indutiva.

Exemplo

Para uma carga ligada em série drenando uma corrente i(t) = 4 cos(100πt + 10°) A, temos uma tensão de v(t) = 120 cos(100πt – 20°) V aplicada. Vamos determinar a potência aparente e o fator de potência da carga, para essa situação:

Começando pela potência aparente:

Já o fator de potência:

Nesse caso, o fator de potência está adiantado, pois a corrente está adiantada em relação à tensão.

Potência complexa

A potência complexa é um importante recurso na análise de potência, isso porque contém todas as informações importantes à potência absorvida por uma determinada carga.

Para entender isso vamos observar o circuito com uma carga CA da Figura 1:

Considerando que a tensão e corrente na forma fasorial serão:

A potência complexa S absorvida pela carga CA será o produto entre a tensão e do conjugado da corrente:

Em valores RMS, temos:

Lembrando que:

Então S pode ser escrito como:

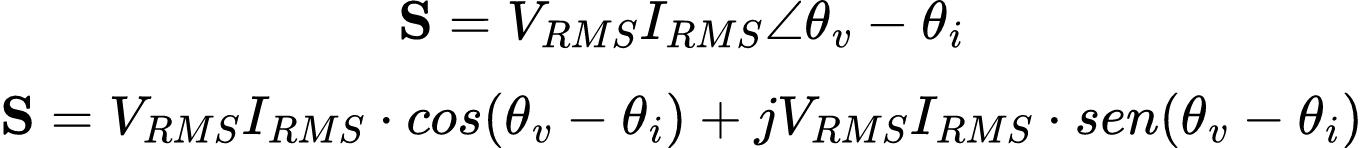
Notamos da equação que a amplitude da potência complexa é igual a da potência aparente, então a potência complexa é medida em volt-ampères (VA). Nota-se também que seu ângulo é o ângulo do fator de potência.

Além disso, a potência complexa pode ser expressa em termos de impedância local Z. Então, assumindo que a impedância da carga Z pode ser escrita como:

Com V_RMS=ZI_RMS, temos que a potência complexa será:

Como Z = R +jX, podemos reescrever:

Em que P é a potência média e depende da resistência da carga, R, já Q depende da reatância da carga, X, e é chamada de potência reativa.

Assim, a potência real P é a potência média em watts liberada para a carga. A potência reativa Q é uma medida de troca de energia entre a fonte e a parte reativa da carga. A unidade de medida de Q é o VAR (volt-ampère reativo), com o intuito de diferenciá-la da potência real cuja unidade é o watt. De acordo com o valor da potência reativa, temos diferentes comportamentos:

• Q = 0 para cargas resistivas (FP unitário);
• Q < 0 para cargas capacitivas (FP adiantado);
• Q > 0 para cargas indutivas (FP atrasado).

Assim, a potência complexa contém todas as informações relevantes de uma determinada carga.

É comum representar S, P e Q na forma de um triângulo, chamado de Triângulo das potências, mostrado na Figura 2a. O qual é similar ao triângulo das potências que mostra a relação entre Z, R e X, ilustrado na Figura 2b.

Triângulo das potências

O triângulo das potências possui quatro parâmetros: potência aparente ou complexa; potência média; potência reativa e ângulo do fator de potência. Com dois desses parâmetros, é possível obter os outros dois a partir do triângulo. 

É importante se atentar ao quadrante do triângulo, isso porque quando S está no primeiro quadrante, temos uma carga indutiva e um fator de potência atrasado. Já quando S está no quarto quadrante, a carga é capacitiva e o fator de potência está adiantado. Caso a potência complexa caia no segundo ou terceiro quadrantes, significa que a impedância da carga tem uma resistência negativa.

Referências

ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.