Técnica dos Mínimos Sinais aplicada ao conversor Boost

09/10/2019

ÍNDICE DE CONTEÚDO

Introdução

A eletrônica de potência está presente nas mais diversas aplicações, desde geração de energia eólica até fonte de computadores, em alta potência e também baixa potência, abrangendo os mais diversos tipos de aplicações.

Um conversos muito comum e bastante utilizado é o BOOST, utilizado para elevar a tensão em circuitos, prometendo também em muitos dos casos uma eficiência maior de conversão.

Este estudo compreende a dinâmica do conversor em sua forma ideal analisando a técnica dos mínimos sinais para extração da função de transferência e verificando também sua resposta ao original.

Também será estudado o controle no domínio da frequência, sendo controle contínuo. Para as malhas de corrente e tensão.

Os Melhores Treinamentos sobre Sistemas embarcados e IoT

Cursos com professores qualificados para acelerar sua carreira e projetos

MATRÍCULE-SE AGORA

Circuito BOOST

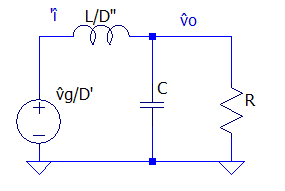
O circuito do conversor BOOST, idealizado, pode ser visualizado na Figura 1, é utilizado para elevar tensões.

Figura 2: Circuito do Conversor Boost com chave fechada (Ciclo de trabalho D).

Figura 3: Circuito do Conversor Boost com chave aberta (Ciclo de trabalho D’).

Este conversor possui dois estados, um com a chave fechada (Figura 2), onde a corrente da fonte energiza o indutor L, o capacitor C e fornecendo corrente para a carga R. Com a chave aberta (Figura 3) a corrente do laço passa através do diodo e o indutor L fornece corrente para carga RC.

Tensão e corrente no indutor (L)

A tensão no indutor quando a chave esta fechada é , e quando está aberta, . Desta maneira, tem-se em regime: , sendo D o ciclo de trabalho (razão entre tempo de chave fechada e período de chaveamento) e T o período da frequência de chaveamento e D’ razão entre o período com chave aberta e período de chaveamento.

$VL=L \frac{di}{dt}\, , logo,\: \frac{VL}{L}= \frac{di}{dt},\, resultando em :\, \frac{Vg}{L}=\frac{di} {T*D}$

Com a tensão do indutor determinada é possível estipular a variação de corrente no indutor, sedo que . Considerando metade da variação da corrente no indutor, tem-se .

iL_{avg}= \frac{Vo}{RD'}= \frac{Vg}{RD'^2}

Assumindo que a corrente em regime do capacitor é , é possível obter a seguinte equação: , no nó onde são conectados L, C e R, tem-se que , logo quando chave aberta e , quando fechada. Resultando na corrente média no indutor igual à .

Desta maneira pode-se calcular a corrente de pico e mínima do indutor: e .

Ganho do conversor

Considerando a tensão do indutor em regime, , obtêm-se .

Corrente tensão e corrente no capacitor

A corrente no capacitor é quando chave aberta e quando fechada. Resultando na corrente média no indutor igual a

\Delta V= \frac{1}{2}\frac{Vo}{R}\frac{1}{C}\frac{D}{f}

A tensão de ripple pode ser determina da seguinte maneira: .

Regime Permanente

\left \langle VL \right \rangle = Vg -VoD' = 0

\left \langle ic \right \rangle= ID'- \frac{Vo}{R} = 0

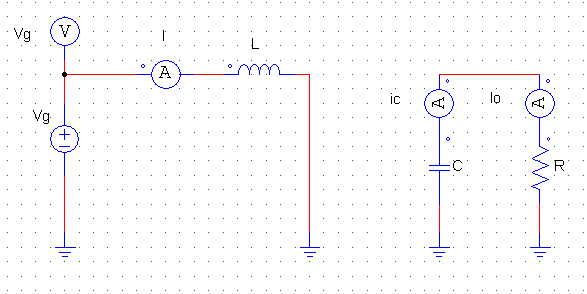
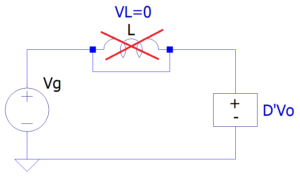
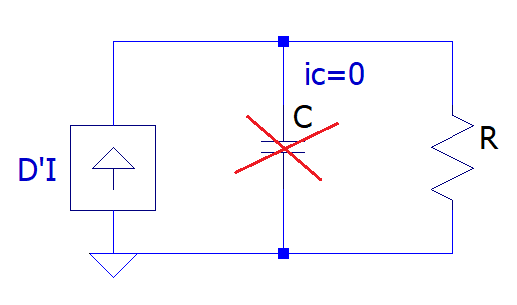
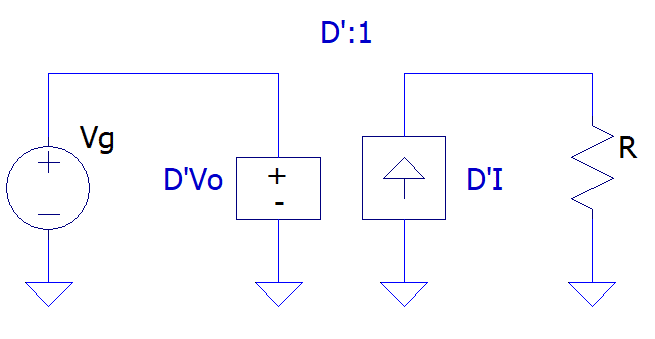
A tensão média em regime permanente do Indutor L é e a corrente no capacitor C, é . Nas Figuras 4 e 5, pode ser visualizada a representação em circuito.

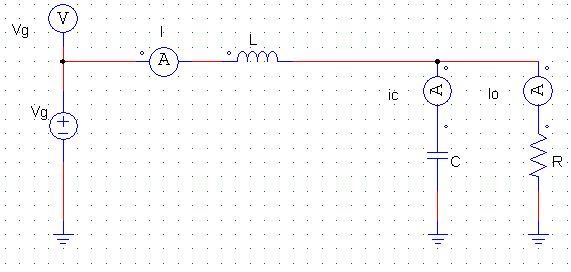
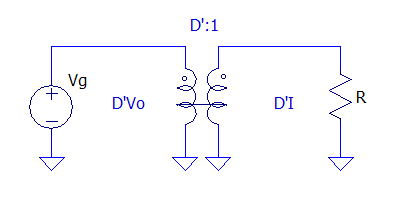
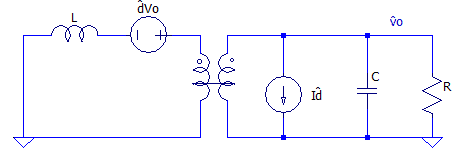
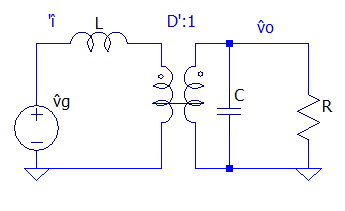
Figura 4: Circuito em regime permanente da tensão no indutor.

Figura 5: Circuito em regime permanente da corrente no capacitor.

Esses circuitos estão indiretamente acoplados, para visualizar essa relação de forma direta, os circuítos das Figuras 4 e 5 são colocados justapostos e finalmente acoplados com um transformador DC, como pode ser visualizado nas Figuras 6 e 7, respectivamente.

Figura 6: Circuito em regime permanente.

Figura 7: Circuito em regime permanente com acoplamento de transformador DC.

Figura 8: Circuito Resultante. Tensão Vg movida para o secundário.

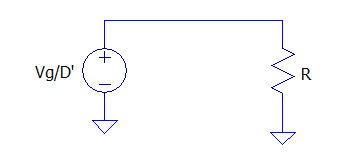
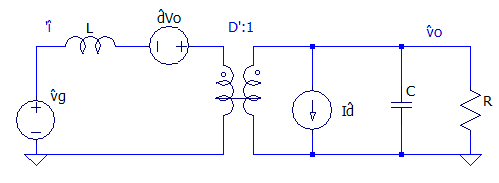
Colocando a fonte de tensão no secundário é possível obter um circuito equivalente, representado pela Figura 8, sendo possível obter a corrente Io, .

Calculo do conversor

As especificações do conversor podem ser visualizadas na Tabela 1. As variáveis de Vg à D, foram especificadas, L,Q,C calculadas.

Tabela 1: Especificações do conversor boost.

Boost
Vg	12	V
Vo	24	V
R	5	ohms
Io	4,8	A
F	50000	hz
T	2E-05	s
ΔiL	0,3	A
ΔvC	0,3	V
D	0,5

L	2,00E-04	H
C	8E-05	F

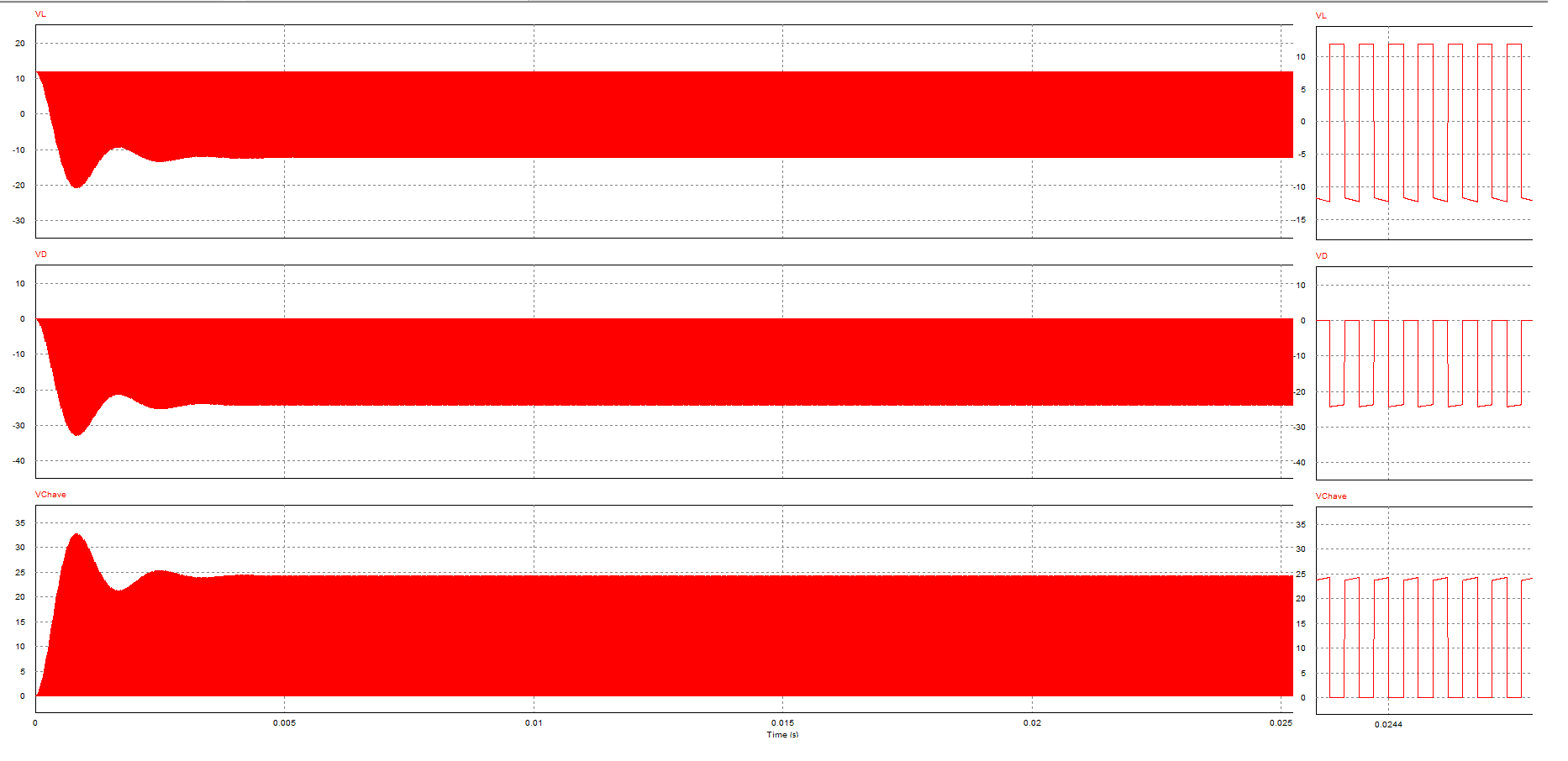
As formas de onda podem ser visualizas nas Figuras 9 à 11.

Figura 9: Tensão na carga e Corrente no Indutor com detalhe.

Figura 10: Corrente no Capacitor e Resisto com detalhe.

Figura 11: Tensão no Indutor; Tensão no Diodo e Tensão na Chave. Com Detalhe.

Mínimos Sinais

Com as equações em regime permanente o próximo passa é inserir as perturbações, da seguinte maneira:

\left \langle Vg(t) \right \rangle= Vg + \hat{vg(t)}

Na fonte:

Ciclo de trabalho:

\left \langle i(t) \right \rangle = I + \hat {i(t)}

Corrente no Indutor:

\left \langle Vo(t) \right \rangle = Vo + \hat {vo(t)}

Tensão na carga:

\left | d(t) \right | \ll \left | D \right |

\left | \hat{i(t)} \right | \ll \left | I \right |

\left | \hat{vo(t)} \right | \ll \left | Vo \right |

\left | \hat{vg(t)}\right | \ll \left | Vg \right |

Sendo:; ; ;

L \frac{d(I+\hat{i(t)})}{ dt }=(Vg+\hat {vg(t)} )(D+\hat {d(t)} )+ (Vg+\hat {vg(t)}-Vo-\hat vo(t))(D'- \hat d(t) )

Com a equação é possível realizar as substituições para inserir as perturbações:

, resolvendo a equação, tem-se:

Termos DC:

D \hat{vg(t)}+D'\hat{vg(t)}-D'\hat{vo(t)}+Vo \hat{d(t)}

Termos de Primeira Ordem:

Termos de segunda Ordem:

L \frac{d \hat{i(t)}} {dt}= Vg(t)-DVo(t) +\hat{d(t)}{Vo(t)}

Utilizando apenas os termos de primeira ordem, a equação linearizada de tensão no indutor é , o circuito pode ser visualizado na Figura 13.

C \frac{d \hat{vo(t)}}{dt}= -D' \hat{i(t)} - \frac{\hat{vo(t)}}{R}+I \hat{d(t)}

De maneira análoga obtêm-se a corrente linearizada no capacitor, resultando em: , o circuito pode ser visualizado na Figura 12.

Figura 12: Circuito Linearizado da corrente no capacitor.

Figura 13: Circuito linearizado da tensão no indutor.

O circuito resultante com transformador DC pode ser visualizado na Figura 14.

Figura 14: Circuito equivalente linearizado do conversor boost.

Funções de transferência

\hat{vo(s)}= G_{vd} \hat{d(t)} +G_{vg} \hat{vg(t)}

\hat{i(s)}= G_{id} \hat{d(t)} +G_{ig} \hat{vg(t)}

Com o circuito linearizado às pequenas variações é possível obter a função de transferência. Para esse circuito é interessante extrair as funções de transferência para a tensão na carga e corrente no indutor para as variações de ciclo de trabalho, sendo essas : e .

G_{vd} ( s )=\frac{\hat{ vo(s)}}{ \hat{d(t)} } \mid \hat{ vg=0 }

A função de transferência , pode ser decomposta em duas partes, primeiramente as variações de tensão de saída devido ao ciclo de trabalho, quando , sendo essa: . (Note que D’’ é nos circuitos).

Figura 15: Circuito para obtenção de G_vd ( s )

Figura 16: Circuito para obtenção de G_vd ( s ) com indutor e fonte transferidos para o secundário.

O circuito da Figura 16 possui uma fonte de tensão e outra de corrente, desta maneira será utilizada superposição para obtenção da função de transferência G_vd ( s ).

G_{vd.vo}( s )= \frac{vo}{D'} \frac{1}{ \frac{s^2 LC}{D'^2} + \frac{s L}{RD'^2}+1}

G_{vd.I}( s )= \frac{-I}{D'^2} \frac{sL}{ \frac{s^2 LC} {D'^2} + \frac{s L}{RD'^2}+1}

G_{vd}( s )= \frac{Vo}{D'} ({1- \frac{sLID'} {D'^2 Vo}}) \frac{1} { \frac{s^2 LC}{D'^2} + \frac{s L} {RD'^2}+1}

A função de transferência obtida para com a fonte de tensão é e para de corrente , resultando em:. A comparação entre a função e modelo comutado pode ser visualizado na Figura 21.

G_{vg} ( s )=\frac{\hat{ vo(s) }}{ \hat{vg(t)} } \mid \hat{ dt=0 }

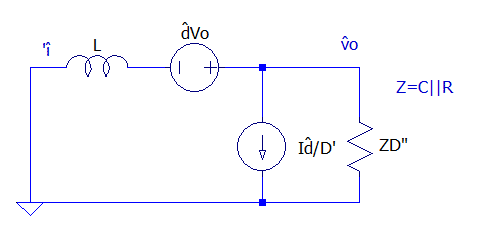
Com obtida é necessário obter , Figura 17 representa o circuito equivalente para obtenção da função de transferência e a Figura 18, com fonte e indutor transferidos para o secundário.

Figura 17: Circuito equivalente para obtenção de G_vg ( s )

Figura 18: Circuito equivalente para obtenção de G_vg ( s ) com fonte e indutor transferidas para o secundário.

G_{vg} ( s )= \frac{1} {D'} \frac{1} { \frac{s^2 LC} {D'^2} + \frac{s L} {RD'^2}+1}

Resultado em . A comparação entre a função e modelo comutado pode ser visualizado na Figura 22.

G_{id} ( s )=\frac{\hat{ i(s) }}{ \hat{d(t)} }\mid \hat{ vg=0 }

G_{id} ( s )= \frac{2Vo}{RD'^2} \frac{1}{\frac{s^2 LC}{D'^2} + \frac{s L}{RD'^2}+1}({1+ \frac{sCR} {2}} )

Agora é necessário obter as funções de transferência para a corrente, sendo essa também composta de duas partes, primeiramente será extraída , o circuito utilizado é o da Figura 15, entretanto com os componentes do secundário transferidos para o primário, conforme Figura 19. Também é utilizado superposição pois há duas fontes, resultando em: . A comparação entre a função e modelo comutado pode ser visualizado na Figura 23.

Figura 19: Circuito linearizado para obtenção de da corrente, com fonte de corrente e carga transferidas para o primário.

G_{iv} ( s )=\frac{\hat{ i(s) }} { \hat{v(t)} } \mid \hat{ dt=0 }

G_{ig} ( s )= \frac{1}{RD'^2} \frac{sCR+1}{\frac {s^2 LC}{D'^2} + \frac{s L}{RD'^2}+1}

As variações de corrente devido à variações da fonte de tensão, , podem ser obtidas utilizando a Figura 17, entretanto com toda a carga do secundário para o primário, conforme Figura 20. Resultando em . A comparação entre a função e modelo comutado pode ser visualizado na Figura 24.

Figura 20: Circuito equivalente para obtenção das variações de corrente pelas da fonte de tensão.

Para analisar as funções de transferência foi posto um estímulo na fonte e no ciclo de trabalho, sendo esse senoidal, com frequência de 100 Hz à 1 Mhz, com picos de 0.01 à 0.02. Estimulando as funções de transferência obtidas e o circuito comutado. O resultado pode ser visualizado nas Figuras: 21, 22, 23 e 24.

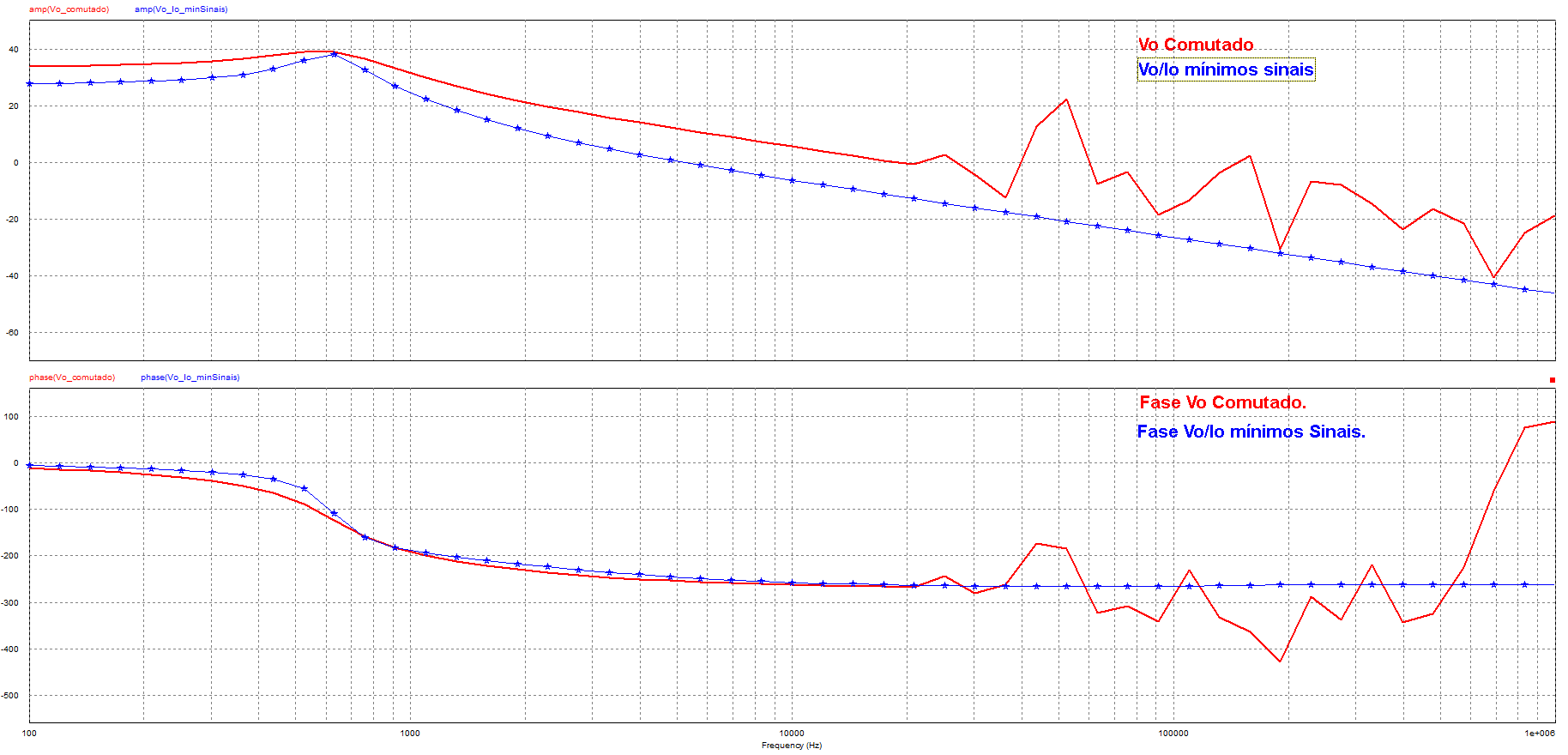
G_{vi}( s )= \frac{RD'}{2} \frac{1-s\frac{L}{RD'^2}}{ 1+s\frac{RC}{2}}

A função entre tensão de saída e corrente é , a resposta em frequência pode ser visualizada na Figura 25.

Ainda é necessário gerar a referência de corrente, tem-se que , resultando em

Figura 21: Comparação da resposta em frequência da função de transferência obtida e circuito comutado, para G_vd ( s ) .

Figura 22: Comparação resposta em frequência da função de transferência obtida e circuito comutado, para G_vg ( s ) .

Figura 23: Comparações da resposta em frequência da função de transferência obtida e circuito comutado, para G_id ( s ).

Figura 24: Comparações da resposta em frequência da função de transferência obtida e circuito comutado, para G_ig ( s ).

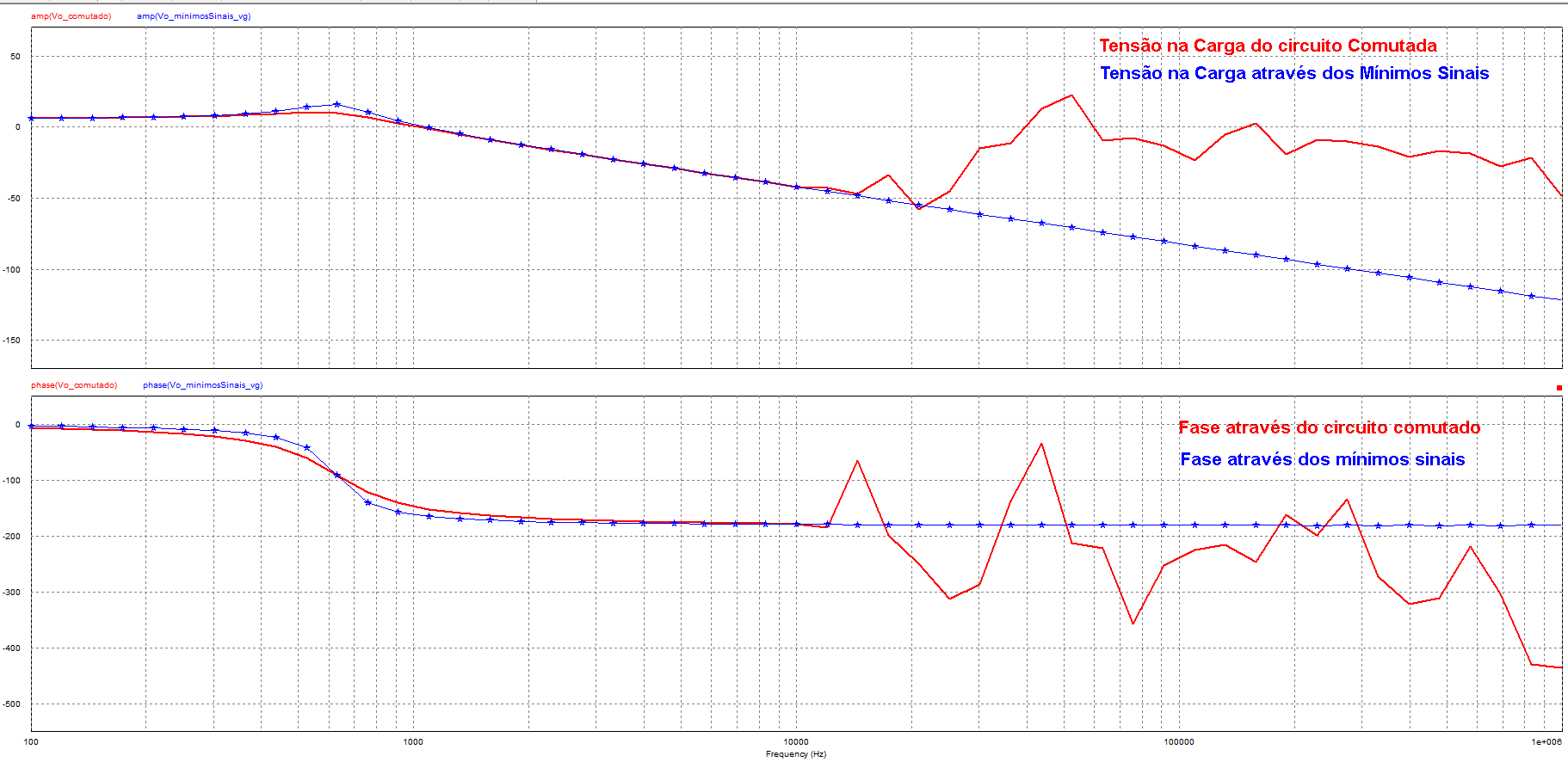
Figura 25: Resposta em frequência da função e modelo comutado. Estimulado por .

Controle

A principal malha do conversor é a de corrente no indutor L. Basicamente o ciclo de trabalho variará e assim controlará a corrente no indutor para variar a tensão na carga. Existem malhas secundárias para controlar a tensão na carga, exercendo referência para a de corrente.

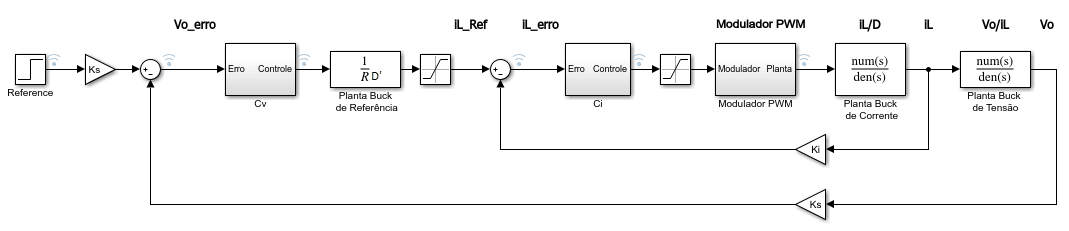
Para o diagrama de controle de Figura 26 são necessárias no mínimo, três plantas para análise dimensionamento dos controladores, sendo essas:

, onde é extraída a razão de corrente no indutor pela razão cíclica sendo que a saída dessa malha é a corrente .

, para assim estipular a variação da tensão da carga, em função da corrente do indutor.

Para a referência de corrente do circuito tem-se que .

As funções de transferência foram apresentadas no capítulo anterior.

O controle do circuito será realizado através do domínio da frequência, inserindo compensadores, verificando ganhos e estabilidade.

Serão analisados o modelo continuo, onde o controle é realizado por controlador PI.

Figura 26: Malha do circuito para controle de corrente e tensão

Controle Contínuo

O circuito de controle pode ser verificado na Figura 27. A função de transferência em laço aberto para o circuito da malha de corrente é dada por (os mesmos valores são utilizados para ambas funções de transferência):

\dpi{100} \fn_cm \small \frac{iL}{D} =G_{iL} K_{PWM} K_i (K_{ci} \frac{(s +W_z ){s}}), onde \: K_i=0.2,K_{pwm}=1,K_{ci}=1,Wz=5000

O gráfico de bode poder ser visualizado na Figura 28.

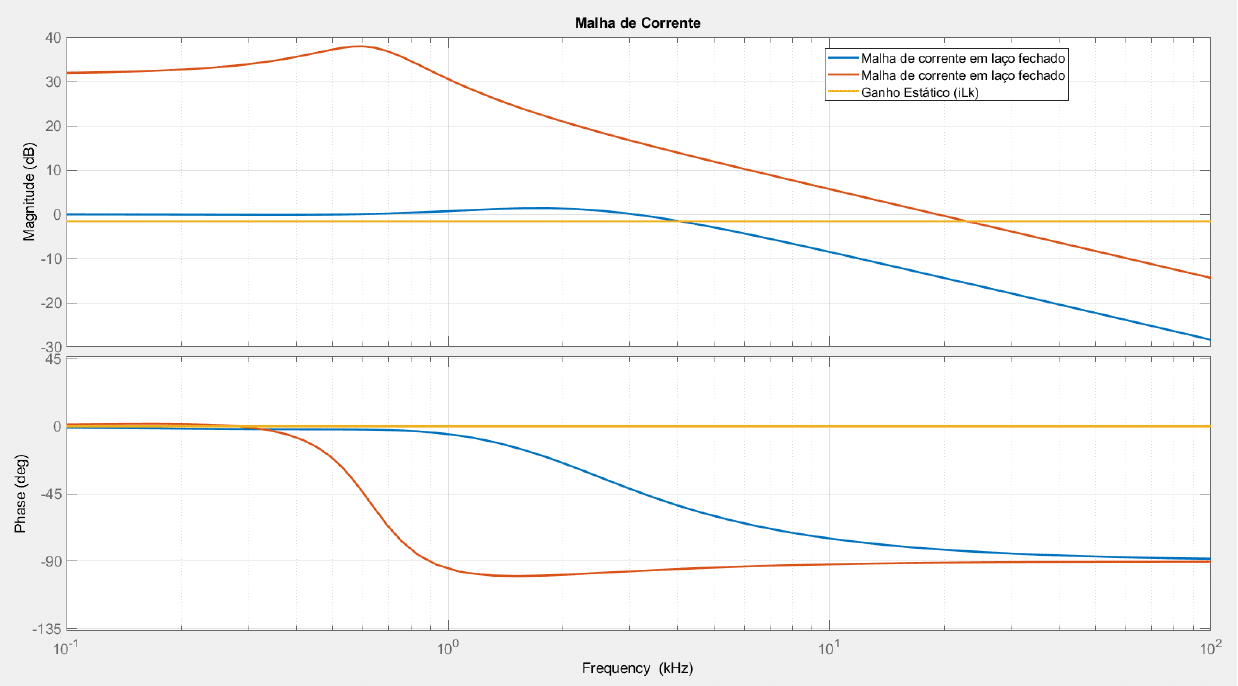
Figura 27: Circuito do conversor boost com malha de corrente e tensão.

Para realizar a análise da malha de tensão é necessário uma função de transferência com ordem superior a segunda, para simplificar, analisa-se a resposta em frequência em laço fechado da malha de corrente, que pode ser visualizado na Figura 28 .

A equação de laço fechado da malha de corrente ,pode ser observada abaixo:

\frac{iL}{iL_{ref}} =\frac{G_{iL} K_{PWM} K_i (K_{ci} \frac{(s +W_z )}{s})}{1 +G_{iL} K_{PWM} K_i(K_{ci} (\frac{s+W_z}{s}))},

onde\: K_i=0.2,K_{pwm}=1,K_{ci}=1,Wz=5000

iL_K= \frac{iL}{iL_{REF}} =\frac{1}{( 1+K_i)}

Através da Figura 28, verifica-se que possui ganho, e pouco significativo, apenas em baixa frequência, sendo assim essa malha será substituída por um ganho estático: , sendo que é o ganho do sensor de corrente.

Figura 28: Resposta em em frequência em laço aberto, fechado da malha de corrente para circuito. Representação de ganho estático que substitui a malha.

Desta maneira é possível obter a função de transferência em laço aberto para a malha de tensão:

iL_{ref} =\frac{iL_k} {RD'} K_v G_{vi} (K_{cv} \frac{(s +W_z )} {s}),

onde\: K_v=0.2,K_{cv}=0.1,Wz=5000,R=5,D'=0.5

O gráfico de bode da equação acima pode ser visualizado na Figura 29.

Figura 29: Diagrama de bode para iL_ref .

O resultado da simulação para os conversores pode ser visualizado nas Figuras 30 . É verificado o comportamento em sobrecarga.

Figura 30: Resultado Obtido na simulação com controladores contínuos e com sobrecarga. Corrente Máxima no indutor de 15A.

Considerações finais

O estudo dos conversores em sua forma ideal é primordial para entendê-lo plenamente. Com esse estudo é possível extrair as principais formas de onda e equações para dimensionamento.

Foi verificado que os modelos adquiridos através da técnica dos mínimos sinais são satisfatórios em relação ao comutado e valem para um ponto de operação do sistema. As simulações do circuito comutado apresentam incoerências em alta frequência, devido ao passo de cálculo, pois foi utilizado um de tamanho maior ao necessário devido ao tempo de simulação ou até um bug na ferramenta, que acontece no mundo real.

O domínio da frequência é uma ferramenta versátil para se dimensionar compensadores, é o possível verificar o ganho em baixas e altas frequências e também se existem várias frequências de corte.

A malha de corrente é muito importante para que o conversor opere com segurança e não ultrapasse a corrente máxima permitida. Claro que fusíveis podem ser postos, no entanto essa proteção faz com o conversor opere em modo de sobrecarga, baixando a tensão de saída e fornecendo a corrente máxima permitida. Avisos podem ser emitidos.

De modo geral as simulações atendem vários requisitos, no entanto ainda é necessário, ausência de carga , perturbação da tensão na fonte, entre outros.