A maioria das cargas domésticas (máquinas de lavar roupa, ar-condicionado e geladeiras) e também as industriais (motores de indução) são indutivas e atuam com um fator de potência baixo, com atraso. Como sua construção não pode ser alterada, podemos aumentar o seu fator de potência.
Esse processo de aumentar o fator de potência, sem fazer uma alteração na tensão ou corrente da carga original, é chamado de correção do fator de potência. Neste artigo, vamos entender como fazer isso.
Correção do fator de potência
Uma carga indutiva é representada por um modelo em que há uma associação em série entre um indutor e um resistor, como mostra a Figura 1.

Como a maioria das cargas é indutiva, o fator de potência de uma carga é aumentado ao se instalar um capacitor em paralelo com a carga, conforme mostrado na Figura 2.

O efeito do acréscimo do capacitor pode ser visualizado com um diagrama de fasores das correntes. Como podemos ver na Figura 3, supondo que o circuito da Figura 1 tenha um fator de potência igual a cos θ1 e o circuito da Figura 2 tenha um fator de potência igual a cos θ2, acrescentar o capacitor fez com que o ângulo fase entre a tensão e a corrente fosse reduzido de θ1 para θ2, aumentando o fator de potência.

Fonte: ALEXANDER (2013).
Observando o tamanho dos vetores, também é possível concluir que, sob a mesma tensão, o circuito da Figura 1 drena uma corrente IL maior que a corrente I absorvida pelo circuito da Figura 2.
Altas correntes resultam em maiores perdas de potência, isso porque ela é um fator ao quadrado já que P = I2LR. Então, é mais interessante tanto para companhias elétricas, quanto para os consumidores minimizar o nível da corrente ou manter o fator de potência o mais próximo possível da unidade.
Por outra perspectiva, podemos ver a correção do fator de potência considerando o triângulo de potência da Figura 4.

Fonte: ALEXANDER (2013).
Se a carga indutiva original tiver potência aparente S1:

Para aumentar o fator de potência de cos θ1 para cos θ2 sem alterar a potência (ou seja,com P = S2cos θ2), então a nova potência reativa será:

A redução na potência reativa é provocada pelo capacitor shunt, então:

O valor da capacitância shunt C necessária é determinada através de:

Observe que a potência real P dissipada pela carga não é afetada pela correção do fator de potência.
Apesar da situação mais comum na prática ser o aparecimento de uma carga indutiva, também é possível que a carga seja capacitiva. Isso significa que a carga está operando com um fator de potência adiantado. Nessa situação, um indutor deverá ser ligado na carga para correção do fator de potência.
Assim, a indutância shunt L necessária será:
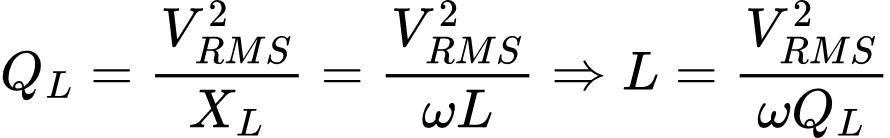
Em que QL = Q1 – Q2 é a diferença entre a potência reativa atual e a anterior.
Exemplo
Para facilitar o entendimento, faremos o seguinte exemplo: quando conectada a uma rede elétrica de 120 V (RMS), 60 Hz, uma carga absorve 4 kW com um fator de potência atrasado de 0,8. Determine o valor da capacitância necessária para elevar o FP para 0,95.
Começamos verificando que para FP=0,8, temos:

Em que θ1 é a diferença de fase entre a tensão e a corrente. Além disso, obtemos a potência aparente a partir da potência real e do FP:
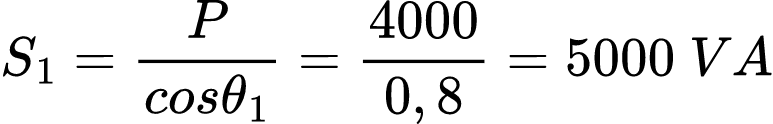
E a potência reativa é:

Com o FP aumentado para 0,95:

A potência real P não irá mudar, já a potência aparente sim. Seu novo valor será:

Então a nova potência reativa é:
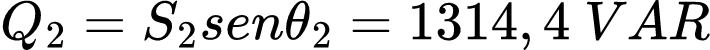
A diferença entre a potência reativa atual (FP=0,95) e a anterior (FP=0,8) se deve ao acréscimo do capacitor em paralelo com a carga. Assim, a potência reativa do capacitor e capacitância são:

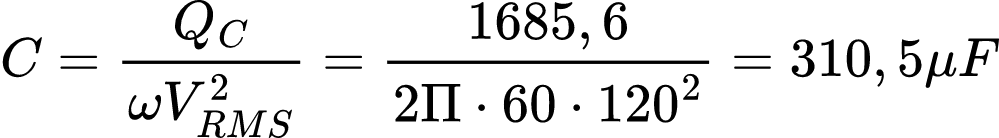
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.

















Parabéns, você é um exemplo de como explanar de uma forma clara um assunto tão importante para nós engenheiros eletricistas!