Conversor Buck – Aspectos ideais e não ideais

A eletrônica de potência está presente nas mais diversas aplicações, desde geração de energia eólica até fonte de computadores, em alta potência e também baixa potência, abrangendo os mais diversos tipos de aplicações.

Um conversor muito comum e bastante utilizado é o BUCK, utilizado para baixar a tensão em circuitos, prometendo também em muitos dos casos uma eficiência maior de conversão.

Este estudo compreende a dinâmica do conversor em sua forma ideal e também alguns componentes que fazem parte da aplicação real e alteram sua forma de funcionamento.

Também será estudado o controle no domínio da frequência, sendo controle contínuo e também discretizado. Para as malhas de corrente e tensão.

Circuito Buck

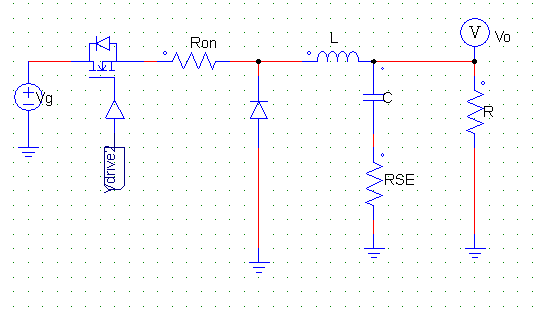
O circuito do conversor Buck, idealizado, pode ser visualizado na Figura 1, é utilizado para baixar tensões.

Este conversor possui dois estados, um com a chave fechada (Figura 2), onde a corrente da fonte energiza o indutor L, carregando o capacitor C e fornecendo corrente para a carga R. Com a chave aberta (Figura 3) a corrente do laço passa através do diodo e a fonte não fornece carga ao circuito.

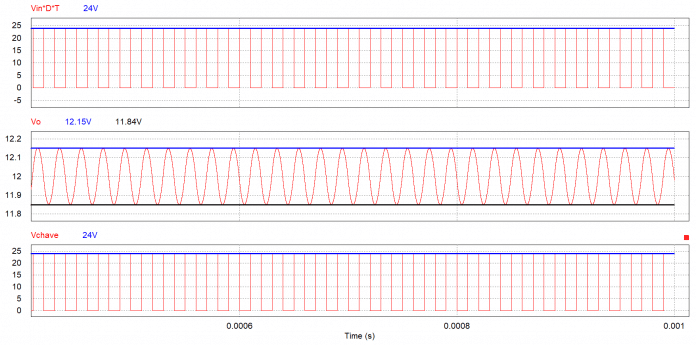
Tensão e corrente no indutor (L)

A tensão no indutor quando a chave esta fechada é , e quando está aberta,. Desta maneira, tem-se em regime:, sendo D o ciclo de trabalho (razão entre tempo de chave fechada e período de chaveamento) e T o período da frequência de chaveamento.

Com a tensão do indutor determinada é possível estipular a variação de corrente no indutor, sedo que resultando em:

Considerando metade da variação da corrente no indutor, tem-se

Assumindo que a corrente em regime do capacitor é , é possível obter a seguinte equação: , no nó onde são conectados L,C e R, tem-se que logo para ambos os ciclos. Resultando em , resultando na corrente média no indutor igual a .

Desta maneira pode-se calcular a corrente de pico e mínima do indutor: e .

Ganho do conversor

Considerando a tensão do indutor em regime, , obtêm-se .

Corrente tensão e corrente no capacitor

A corrente no capacitor é para ambos os ciclos. Para o ciclo , tem-se que , analogamente para , tem-se que .

A tensão de ripple pode ser determina da seguinte maneira: .

Calculo do conversor

As especificações do conversor podem ser visualizadas na Tabela 1. As variáveis de Vg à D, foram especificadas, L, Q, C calculadas.

Tabela 1: Especificações do conversor BUCK.

	BUCK
Vg	24	V
Vo	12	V
R	5	ohms
Io	2,4	A
F	50000	Hz
T	2E-05	s
ΔiL	0,3	A
ΔvC	0,3	V
D	0,5
L	200,00E-06	H
Q	1,50E-06	C
C	5,00E-06	F

Malha de Controle para corrente iL e tensão Vo

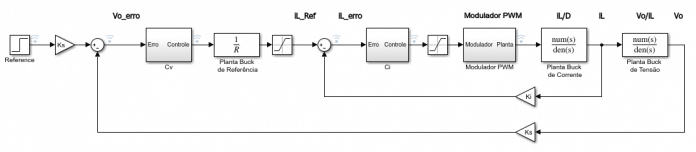
A principal malha do conversor é a de corrente no indutor L. Basicamente o ciclo de trabalho variará e assim controlará a corrente no indutor para variar a tensão na carga. Existem malhas secundárias para controlar a tensão na carga, exercendo referência para a de corrente.

Para o diagrama de controle de Figura 7 são necessárias no mínimo, três plantas para análise dimensionamento dos controladores, sendo essas:

onde é extraída a razão de corrente no indutor pela razão cíclica sendo que a saída dessa malha é a corrente .

, para assim estipular a variação da tensão da carga, em função da corrente do indutor.

Para a referência de corrente do circuíto tem-se que , sendo assim a planta para referência é .

Função de transferência – Corrente Indutor L

Serão avaliadas duas funções de transferência, uma ideal, respectiva do circuito da Figura 1 e outra que considera a resistência da chave e do capacitor, Ron e Rse respectivamente (dito “real”), extraída da Figura 8. Ambas para extrair a função de transferência para corrente no indutor L.

Função de transferência da Figura 1:

Função de transferência da Figura 8:

A resposta em frequência pode ser visualizada no diagrama de bode da Figura 9 e ao estímulo para ambas as funções de transferência na Figura 10.

Função de transferência – Tesão na Carga (C||R) e (C+RSE||R)

Para a tensão de carga, ambas as funções de transferência podem ser encontradas abaixo:

Função de transferência da Figura 1:

Função de transferência da Figura 8:

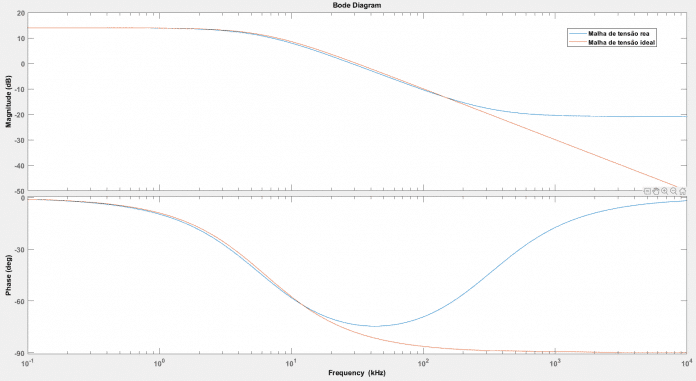
A resposta em frequência pode ser visualizada na Figura 11.

Controle do conversor

O controle do circuito será realizado através do domínio da frequência, inserindo compensadores, verificando ganhos e estabilidade.

Serão analisados o modelo continuo, onde o controle é realizado por um controlador PI, e outro discretizado, em código C. Apenas serão realizadas simulações para ambas as plantas, a ideal e dita “real”

Controle Contínuo

O circuito de controle pode ser verificado na Figura 12, sendo que representa o circuito “real” em controle continuo, para o ideal basta desconsiderar a resistências Ron e RSE, ou considerar igual a zero.

A função de transferência em laço aberto para o circuito da malha de corrente é dada por (os mesmos valores são utilizados para ambas funções de transferência)):

O gráfico de bode poder ser visualizado na Figura 13.

Para realizar a análise da malha de tensão é necessário uma função de transferência com ordem superior a segunda, para simplificar, analisa-se a responta em frequência em laço fechado da malha de corrente, que pode ser visualizado na Figura 14 .

A equação de laço fechado da malha de corrente ,pode ser observada abaixo:

Através da Figura 14, verifica-se que possui ganho, e pouco significativo, apenas em baixa frequência, sendo assim essa malha será substituída por um ganho estático:, sendo que é o ganho do sensor de corrente.

Desta maneira é possível obter a função de transferência em laço aberto, para se obter a referência de corrente através da malha de tensão:

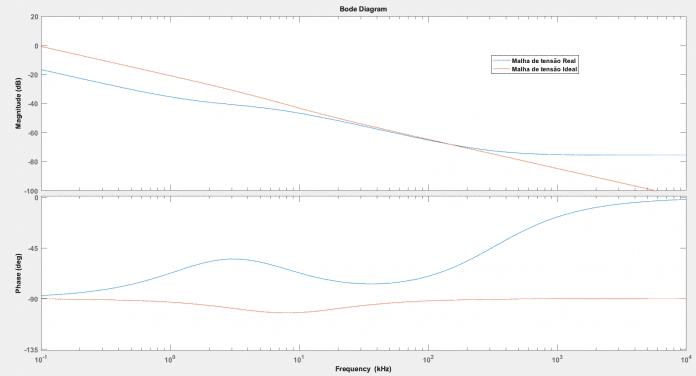
O gráfico de bode da equação acima pode ser visualizado na Figura 15.

Figura 15: Diagrama de bode para . Circuito ideal e real.

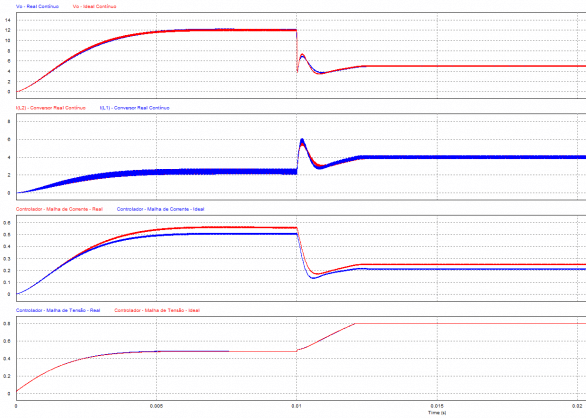
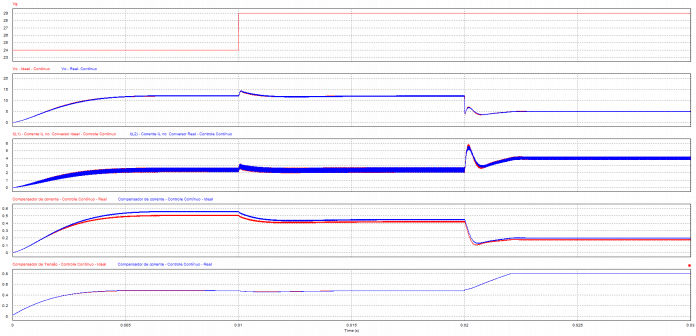
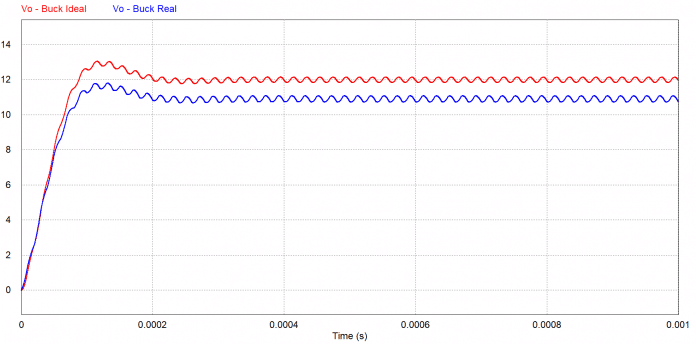
O resultado da simulação para os conversores pode ser visualizado nas Figuras 16 e 17. É verificado o comportamento em sobrecarga e também com perturbação da tensão da fonte.

Discretização dos compensadores

O compensador PI possui a seguinte resposta , no domínio da frequência.

Utilizando a transformada Z, onde e , é possível discretizar o compensador: .

Sendo, e .

Código em C para compensador de corrente do indutor

double Ek;
static double Ek_1=0;
double Uk;
static double Uk_1=0;
double vIn;
double Kci;
double Ts;
double Wz;
double a;
double b;

Kci=0.1;
Ts=0.000005;
Wz=15873;


a=(2*Kci+Kci*Wz*Ts)/2;
b=(-2*Kci+Kci*Wz*Ts)/2;

Ek= Vref-Vout;
Uk=Uk_1+Ek*a+Ek_1*b;

Uk_1=Uk;
Ek_1=Ek;

Código em C para compensador de corrente da tensão

double Ek;
static double Ek_1=0;
double Uk;
static double Uk_1=0;
double vIn;
double Kcv;
double Ts;
double Wz;
double a;
double b;

Kcv=0.01;
Ts=0.000005;
Wz=10000;


a=(2*Kcv+Kcv*Wz*Ts)/2;
b=(-2*Kcv+Kcv*Wz*Ts)/2;

Ek= Vref-Vout;
Uk=Uk_1+Ek*a+Ek_1*b;

Uk_1=Uk;
Ek_1=Ek;

Resultado obtido com controlador discretizado

O resultado obtido no modelo discretizado pode ser visualizado na Figura 18, tensão de saída com perturbação da fonte de tensão e saída do controlador. A única alteração em relação ao circuito contínuo é o controlador.

Considerações finais

O estudo dos conversores em sua forma ideal é primordial para entendê-lo plenamente. Com esse estudo é possível extrair as principais formas de onda e equações para dimensionamento. No entanto, existem aplicações em que esses modelos não são suficientes e são utilizados alguns que se assemelham mais de um conversor real, um exemplo seria um Buck que converte 5V para 1,8V.

Para os modelos utilizados foi verificado que a resistência Ron e RSE, diminuem o ganho do conversor, embora utilizado um valor muitas vezes considerado alto. Em aplicações que requerem alto desempenho pode ser que exista muita diferença da planta calculada com o conversor real, pois conforme visualizado, o controlador necessita um ciclo de trabalho maior no modelo com RSE e Ron. Além do que, essas variáveis fazem com que exista queda de tensão no circuíto.

O domino da frequência é uma ferramenta versátil para se dimensionar compensadores, é o possível verificar o ganho em baixas e altas frequências e também se existem várias frequências de corte.

A malha de corrente e muito importante para que o conversor opere com segurança e não ultrapasse a corrente máxima permitida. Claro que fusíveis podem ser postos, no entanto essa proteção faz com o conversor opere em modo de sobrecarga, baixando a tensão de saída e fornecendo a corrente máxima permitida. Avisos podem ser emitidos.

De modo geral as simulações atendem vários requisitos, no entanto ainda é necessário, ausência de carga , entre outros.

Referências

SLOA049B – Application note texas.

Franklin, Gene F. , Powell, J. David. Feedback Control of Dynamic Systems, 4th Edition . Prentice Hall; 4th edition (January 15, 2002).

Buso, Simone. Mattavelli, Paolo. Digital Control in Power Electronics.

Erickson, Robert W. , Maksimovic. Dragan. Fundamentals of Power Electronics 2nd ed.

BARBI, I. Projetos de fontes chaveavas. 2.ed.Florianopolis: Ed. Do Autor, 2007. 334.