Anteriormente, estudamos circuitos com um único componente de armazenamento e resistores, chamados de circuito RC e circuito RL. Estes eram conhecidos como circuito de primeira ordem, pois as equações diferenciais que os descrevem são de primeira ordem.
Agora conheceremos os circuitos que contém dois componentes de armazenamento e resistores (RLC), os quais são chamados de circuitos de segunda ordem, pois são descritos por equações diferenciais com derivadas segundas.
Neste artigo analisaremos o comportamento dos circuitos RLC em série que são excitados pelas condições iniciais dos componentes de armazenamento, ou seja, eles não irão conter fontes independentes, apesar de poder conter fontes dependentes. E depois, vamos avaliar o comportamento dos circuitos submetidos a uma fonte independente.
Circuitos RLC em série sem fonte
Entender a resposta natural do circuito RLC em série é de suma importância para trabalhar nas áreas de projeto de filtros e de redes de comunicação.
Diante disso, considerando o circuito RLC em série mostrado na Figura 1, observamos um circuito que é excitado pela energia inicialmente armazenada no capacitor e indutor. A tensão inicial é representada por V0 no capacitor e pela corrente inicial I0 no indutor.

Assim, em t = 0:

Ao aplicar a LKT no circuito da Figura 1, temos:
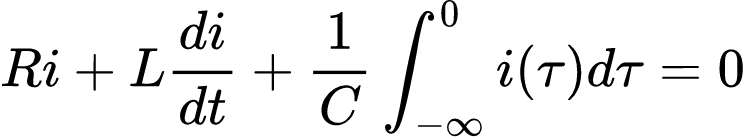
Para remover a integral, diferenciamos em relação a t e reorganizamos os termos para deixar no formato de equação diferencial de segunda ordem.
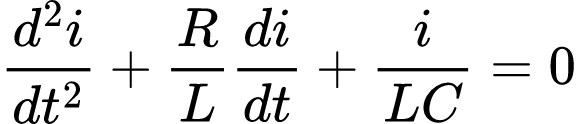
E justamente por ser uma equação diferencial de segunda ordem, os circuitos RLC são chamados circuitos de segunda ordem. Para resolvermos uma equação diferencial de segunda ordem são necessárias duas condições iniciais: o valor inicial de i e sua primeira derivada ou os valores iniciais de i e v.
Como sabemos que o valor inicial de i é I0. É possível obter o valor inicial da derivada de i:

Com as duas condições iniciais é possível resolver a equação diferencial. Relembrando os artigos de circuito RC e RL, de primeira ordem, é plausível concluir que a solução é na forma exponencial.

Em que A e s são constantes a serem determinadas.
Substituindo na equação diferencial de segunda ordem, temos:
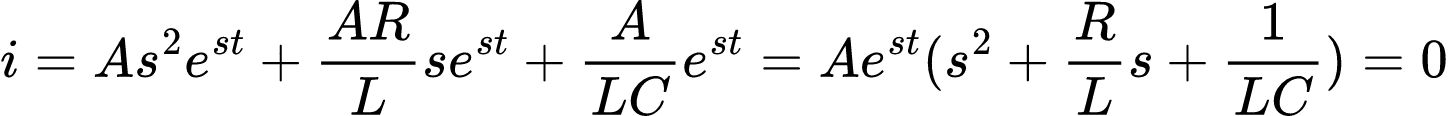
Diante do fato que i = Aest é a solução que estamos buscando encontrar, somente a expressão entre parênteses pode ser igual zero.

Essa a equação quadrática é conhecida como equação característica da equação diferencial, pois as raízes da equação descrevem as características básicas de i.
Uma outra forma mais de expressar as raízes é através de α e ω0:

Em que:

Isso porque as raízes s1 e s2 são chamadas frequências naturais (cuja unidade é (Np/s) nepers por segundo), por estarem associadas à resposta natural do circuito. Então, ω0 é conhecido como frequência natural não amortecida ou frequência ressonante com unidade dada em radianos por segundo (rad/s), e α é o fator de amortecimento ou frequência de neper com unidade nepers por segundo.
Assim, em termos de α e ω0, a equação característica pode ser reescrita como:

Como há dois valores de s, há duas soluções possíveis para i. Onde cada uma delas estará na forma da solução pressuposta, ou seja:

Como a equação inicial encontrada é linear, a solução completa de i é uma combinação linear de i1 e i2. Logo, a resposta natural do circuito RLC em série:

Em que as constantes A1 e A2 são determinadas a partir dos valores iniciais i(0) e di(0)/dt.
Dependendo dos valores de α e ω0 é possível ter três tipos de soluções:
- Caso de amortecimento supercrítico (α > ω0)
Para α ser maior ω0 é preciso que:

Quando isso ocorre, as raízes s1 e s2 são negativas e reais. A resposta, então, é:

Essa resposta decai e se aproxima de zero a cada vez que t aumenta. A Figura 2 mostra a resposta característica para o amortecimento supercrítico.
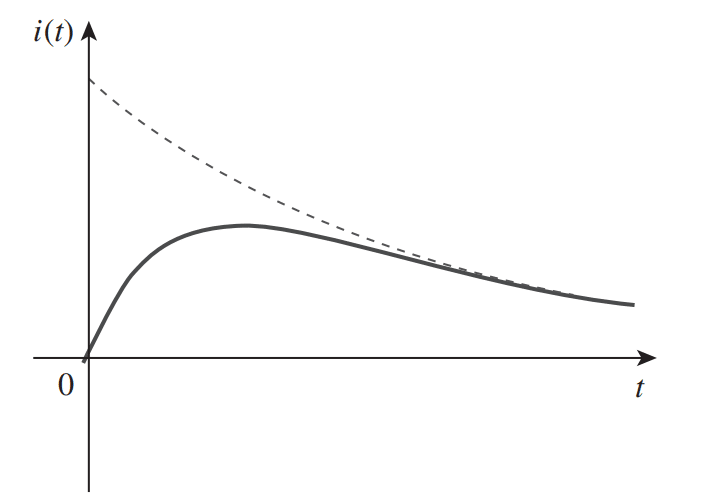
Fonte: ALEXANDER (2013).
- Caso de amortecimento crítico (α = ω0)
Quando α = ω0:

Isso implica em duas raízes (s1 e s2) reais e iguais. Logo:

Nesse caso, a resposta é:

Assim, a resposta natural de um circuito com amortecimento crítico é a soma de dois termos, dentre eles um linear. Graficamente temos o comportamento mostrado na Figura 3.

Fonte: ALEXANDER (2013).
Caso de subamortecimento (α < ω0)
Quando α < ω0:

Isso implica em duas raízes (s1 e s2) complexo conjugadas. Logo:

Em que:

ωd é chamado de frequência de amortecimento. Lembrando que ω0 é chamada frequência natural não amortecida, já ωd é chamada frequência natural amortecida.
A resposta natural, nesse caso, é:

Em que:

Como além da exponencial temos as funções seno e cosseno, a resposta natural para esse caso é amortecida exponencialmente e oscilatória por natureza, como mostra a Figura 4.
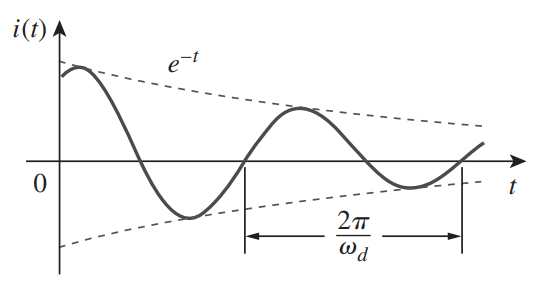
Fonte: ALEXANDER (2013).
Assim, em resumo:
O comportamento desses circuitos podem ser compreendidos pelo conceito de amortecimento, ou seja, a perda gradual da energia inicial armazenada ao longo do tempo;
O efeito de amortecimento se deve à presença da resistência R e o fator de amortecimento α determina a taxa em que a resposta é amortecida:
- Então se R = 0, significa que α = 0. Assim, temos um circuito LC com 1/√(LC) como frequência natural não amortecida;
- Como nesse caso, α < ω0, a resposta além de não amortecida é também oscilatória;
- Nesse caso dizemos que o circuito está sem perdas, pois o elemento amortecedor (R) não está presente.
A resposta oscilatória é possível por existir dois tipos de elementos de armazenamento no circuito.
Exemplo RLC em série sem fonte
Considerando a Figura 5, vamos calcular as raízes características do circuito e determinar se a resposta natural é do tipo amortecimento supercrítico, com subamortecimento ou com amortecimento crítico.

Primeiro, vamos determinar α e ω0:

Como α > ω0, a resposta será do tipo amortecimento supercrítico, com duas raízes reais e negativas. Estas raízes são:
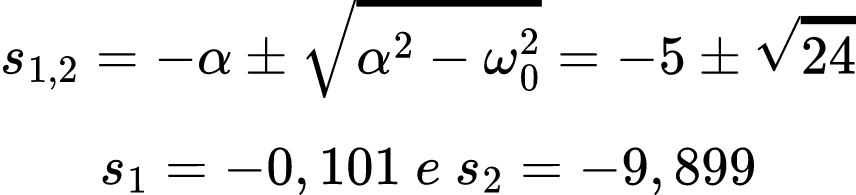
Resposta a um degrau de um circuito RLC em série
A resposta a um degrau é obtida ao aplicar, de forma repentina, uma fonte CC. Consideremos o circuito RLC em série, mostrado na Figura 6.

Aplicando a LKT no circuito para t > 0:

Como i é dado por:

Então, temos:

A equação encontrada tem a mesma forma da equação para o circuito sem fonte de tensão. Ao observar com atenção, vemos que os coeficientes são os mesmos, mas, a variável é diferente.
Portanto, a equação característica para o circuito RLC em série não é afetada pela presença da fonte CC.
A solução para a equação possui duas componentes: uma resposta transiente vt(t) e resposta de estado estável vss(t).

A resposta transiente é a mesma obtida para o circuito sem fonte. Então, considerando a resposta transiente vt(t) para os casos de:
- Amortecimento supercrítico (α > ω0)
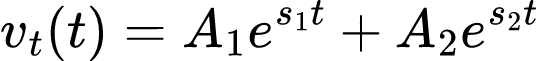
- Amortecimento crítico (α = ω0)

- Subamortecimento (α < ω0)

Com relação a resposta de estado estável, ela é o valor final de v(t). Então no circuito da Figura 6, o valor final da tensão no capacitor é igual ao da fonte de tensão vs. Portanto:

Diante disso as soluções completas para cada caso serão:
| Resposta Completa | Tipo |
| Amortecimento supercrítico | |
| Amortecimento crítico | |
| Subamortecimento |
Lembrando que os valores das constantes A1 e A2 são obtidos das condições iniciais, nesse caso de v(0) e dv(0)/dt.
Outro ponto importante é que v e i são, respectivamente, a tensão no capacitor e a corrente que atravessa o indutor. Então, a equação que obtemos se aplica somente para determinar v.
Mas, uma vez que a tensão no capacitor (vC = v) for conhecida, é possível determinar a corrente i = Cdv/dt, que será a mesma corrente através dos 3 elementos passivos. Portanto, a tensão no resistor é vR = iR, já a tensão no indutor é vL = Ldi/dt.
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.














Muito interessante esta aplicação de equacoes diferenciais