Além dos resistores, um dos componentes elétricos mais comuns são os capacitores, sendo amplamente utilizados em eletrônica, comunicações, computadores e sistemas de potência. Assim como o resistor, o capacitor é um componente de dois terminais, mas suas características são totalmente diferentes daquelas de um resistor.
Neste artigo, vamos entender as particularidades e o funcionamento dos capacitores.
Características do Capacitor
O capacitor manifesta suas características somente quando ocorre uma alteração na tensão ou na corrente do circuito. Enquanto no resistor toda a potência fornecida é dissipada na forma de calor, em um capacitor ideal a energia fornecida é armazenada de forma que pode ser reutilizada no sistema.

A construção básica dos capacitores é bastante simples. Relembrando os conceitos de campo elétrico, temos que este é representado pelas linhas de campo, as quais são traçadas para indicar a intensidade do campo elétrico em qualquer ponto ao redor do corpo carregado.
No artigo de Campo Elétrico consideramos apenas as distribuições das linhas de campo de cargas esféricas positivas e negativas, mas a análise do campo pode ser ampliada para superfícies carregadas de qualquer tamanho e formato. Por exemplo, duas placas paralelas feitas de alumínio (o metal mais comum na confecção de capacitores) estão conectadas a uma bateria através de um resistor e de uma chave, como mostrado na Figura 2.

Fonte: Adaptado de ALEXANDER; SADIKU, 2013.
Considerando que as placas estão inicialmente descarregadas e também que a chave está aberta, nenhuma carga (seja positiva ou negativa) será encontrada nas placas. Mas, no instante em que a chave é fechada, os elétrons são atraídos da placa azul (superior) para o terminal positivo da bateria, percorrendo o resistor, algo que gera uma carga positiva na placa superior. Com mesma intensidade, os elétrons são repelidos pelo terminal negativo em direção à placa cinza (inferior) pelo condutor inferior.
Esse deslocamento de elétrons continua até que a diferença de potencial entre as placas e a tensão da bateria seja a mesma. E o resultado é uma carga positiva na placa azul e uma carga negativa na placa cinza.
Capacitância
É importante ressaltar que o fluxo de cargas ocorre da bateria e do resistor, e não há passagem de elétrons na região entre as placas, ou seja, há um circuito aberto entre as placas do capacitor. A partir dessa análise é possível definir capacitância como:
A medida da quantidade de carga que o capacitor é capaz de armazenar em suas placas, isto é, a sua capacidade de armazenamento. Quanto maior a capacitância, maior a quantidade de cargas armazenadas (maior a capacidade de armazenamento).
A relação entre a tensão aplicada, a carga nas placas e a capacitância é definida pela equação:

- C – capacitância (F – farad)
- Q – carga (C)
- V – tensão (V)
Assim um capacitor possuirá uma capacitância de 1 farad se uma carga de 1 coulomb (6,242·1018 elétrons) for depositada em suas placas com uma diferença de potencial de 1 volt entre elas.
Apesar da capacitância ser a razão entre a carga por placa e a tensão aplicada, ela não depende de nenhuma das duas para armazenar mais ou menos cargas. Na verdade, o fator determinante para o quanto o capacitor pode armazenar são as suas dimensões físicas. Dessa forma, para o capacitor de placas paralelas, por exemplo, capacitância é dada por:
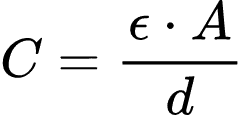
- A – a área de cada placa (m2)
- d – a distância entre as placas (m)
- ϵ – a permissividade do material dielétrico entre as placas (F/m)
Embora seja aplicável somente a capacitores com placas paralelas, da equação podemos inferir que 3 parâmetros são importantes para definir a capacitância: a área das placas, quanto maior a área, maior a capacitância; o espaço entre as placas, quanto menor o espaçamento, maior a capacitância e a permissividade do material, quanto maior a permissividade, maior a capacitância.
É importante se atentar que a maioria dos capacitores está na faixa do µF, nF ou pF é pouco provável que esteja na faixa de 1F ou mais. Isso porque, um capacitor de 1 F pode ser tão grande quanto uma lanterna, enquanto, a maioria dos capacitores usados em sistemas eletrônicos é do tamanho da unha de um polegar (ou menor).
Dielétricos e Permissividade
Diferentes materiais podem ser inseridos entre placas para estabelecerem quantidades de carga adicional nas placas distintas. O objetivo é minimizar a intensidade do campo elétrico entre as placas, para aumentar a carga nelas e, por consequência, aumentar a capacitância.
Mas nem todo material pode ser utilizado, para exercer esse papel é preciso ser isolante e tem de poder estabelecer um campo elétrico no interior da estrutura. Na Tabela 1 temos os materiais mais utilizados.
| Dielétricos | ϵr – valores médios |
| Vácuo | 1,0000 |
| Ar | 1,0006 |
| Teflon | 2,0000 |
| Papel parafinado | 2,5000 |
| Borracha/Poliestireno | 3,0000 |
| Óleo | 4,0000 |
| Porcelana | 6,0000 |
| Baquelite/Óxido de alumínio | 7,0000 |
| Vidro | 7,5000 |
| Cerâmica | 20 – 7500 |
Fonte: (ALEXANDER; SADIKU, 2013).
Todos os materiais mostrados na Tabela 1 são conhecidos como dielétricos, onde “di” vem de oposição e “elétrico” vem de campo elétrico. Já o ϵ é chamado de permissividade, que é uma medida do quão facilmente um material permite compor um campo elétrico em seu meio.
Já o ϵr é chamado de permissividade relativa ou constante dielétrica, cujo intuito é comparar a permissividade de um material com a do ar. O ar é utilizado como referência, então a porcelana com permissividade relativa de 6, permite que um campo elétrico de oposição ao material seja seis vezes melhor do que no ar.
A permissividade do ar é definida como ϵ0 (8,85·10-12 F/m), definimos a permissividade relativa de um material com uma permissividade ϵ como:
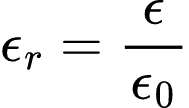
Logo a permissividade ϵ, é dada por:

Referência
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.

















Olá ! Sthefania Fernandes, tudo bem conteúdo bem elaborado gostei muito ….parabéns.
Obrigada, Agnaldo Cosme 🙂