Após cerca de 43 anos da publicação do teorema de Thévenin, E. L. Norton, um engenheiro norte-americano propôs um teorema semelhante. O teorema de Norton afirma que:
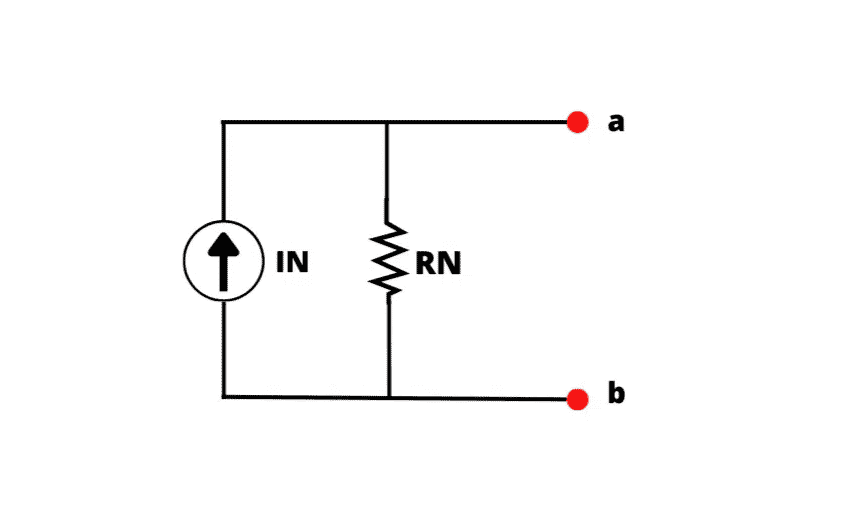
Um circuito linear de dois terminais pode ser substituído por um circuito equivalente formado por uma fonte de corrente IN em paralelo com um resistor RN.
Neste artigo discutiremos mais sobre a aplicação desse teorema e sua relação com o Teorema de Thévenin.
Entendendo o Teorema de Norton
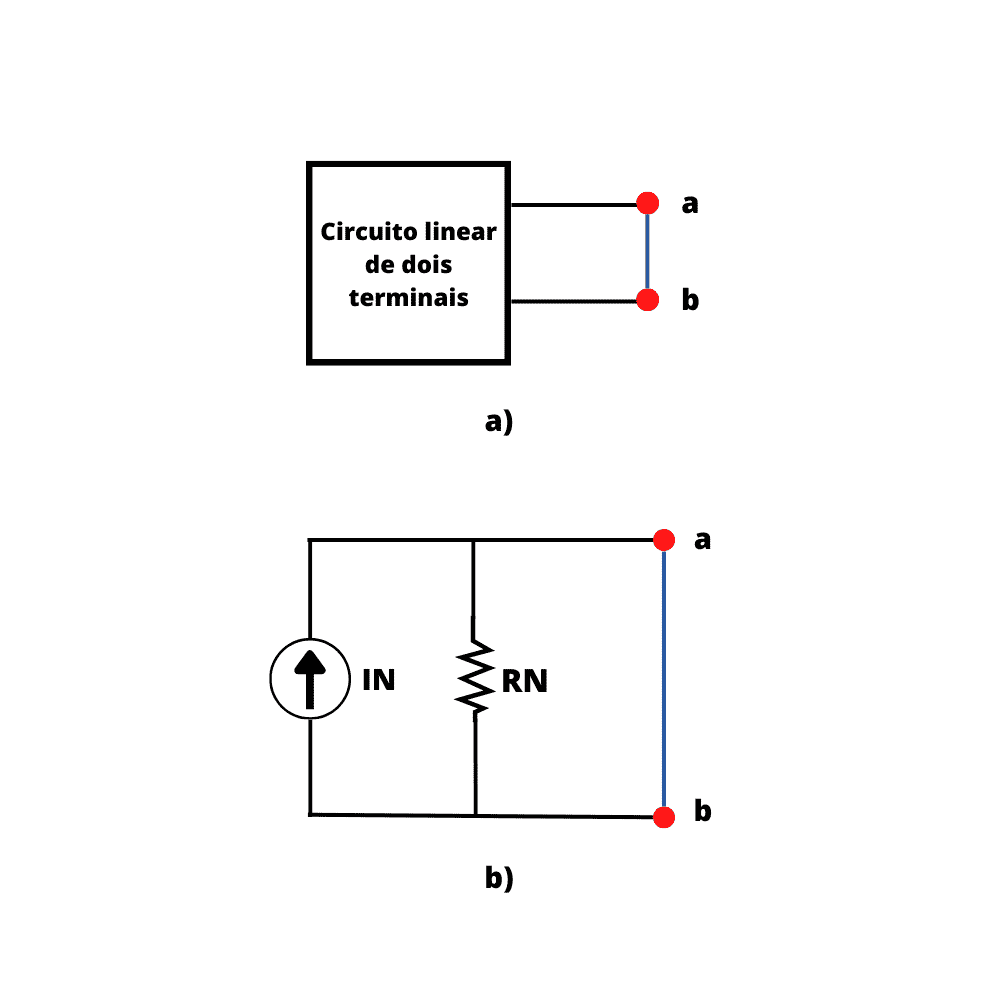
O teorema de Norton permite que o circuito mostrado na Figura 1a, seja substituído pelo circuito da Figura 1b.

Para realizar a conversão é necessário obter os valores de IN e RN. O RN é determinado da mesma forma que obtemos a RTh, ou seja, a resistência equivalente do circuito inativo é igual à RN. Outro detalhe importante é que através da transformação de fontes conclui-se que as resistências de Thévenin e de Norton são iguais.
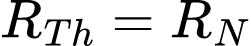
Já para determinar a corrente de Norton IN, precisamos curto-circuitar os terminais a e b dos dois circuitos mostrados na Figura 1. A corrente de curto-circuito na Figura 2b é IN, para a equivalência de circuito ser verdadeira esta corrente deve ser igual à corrente de curto-circuito (ICC) entre os terminais a e b da Figura 2a.
Assim, temos que:

Como temos que RN = RTh, pode-se observar que:
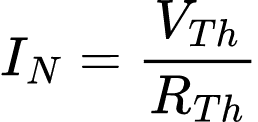
Isso mostra o quão relacionados estão os dois teoremas. Além de ser basicamente, uma transformação de fontes. Por causa disso, muitas vezes a transformação de fontes é chamada transformação Thévenin-Norton.
Procedimento do teorema de Norton
Sabendo que IN é a corrente de curto-circuito através dos terminais e RN é a resistência equivalente nos terminais quando as fontes independentes forem desligadas, há uma série de passos que o levarão ao valor adequado de cada parâmetro do circuito equivalente.
O procedimento é o seguinte:
- Remova a parte do circuito em que se objetiva obter o equivalente de Norton;
- Para calcular RN, realiza-se o mesmo procedimento de RTh:
- Desliga-se as fontes independentes (fontes de tensão são substituídas por curto circuito e fontes de corrente por circuitos abertos);
- Determine a resistência equivalente entre os dois terminais escolhidos.
- Calcule IN:
- Volte a considerar os valores das fontes de tensão e de corrente;
- Determine a corrente entre os dois terminais escolhidos em curto-circuito.
Aplicação do Teorema de Norton
Para fixar o teorema de Norton, vamos determinar o circuito equivalente de Norton do circuito mostrado na Figura 3.

Seguindo os passos do procedimento, para determinar RN é preciso que as fontes independentes sejam zeradas. Assim, obtemos o circuito da Figura 4 e encontramos RN.

Realizando as associações em paralelo e em série, foi encontrado o RN.
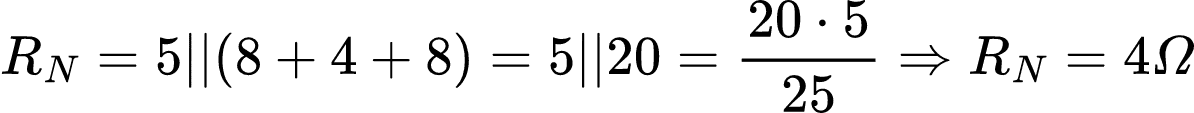
Já para encontrar o IN foi preciso religar as fontes e curto-circuitar os terminais a e b, conforme mostrado na Figura 5. Além disso, aplicamos a análise das malhas para obter a corrente de Norton, considerando positivo percorrer do potencial positivo para o negativo.

Note que o resistor de 5Ω está na cor cinza, pois ele foi curto-circuitado, dessa forma, ele será desconsiderado dos cálculos.
Da malha 1 sabemos que:

Da malha 2 encontramos:
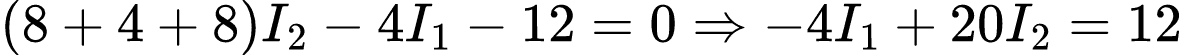
Usando o método da substituição, temos:

Logo o circuito equivalente de Norton é o mostrado na Figura 6.

Referencias
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.