Esse somador utiliza uma técnica para aceleração do cálculo do carry. Em cada estágio ele calcula seu próprio bit–carry de entrada a partir das entradas do primeiro estágio, ou seja, ele não espera a propagação das informações dos estágios anteriores.
Por contra, ele também possui desvantagens, como, por exemplo, o crescimento quase exponencial do número de portas utilizadas a cada estágio, encarecendo e tornando o transporte do carry mais lento para um projeto de mais de quatros estágios.
Devido a essas circunstâncias esse somador é geralmente projetado para somar palavras de 4 bits. Dessa forma, podemos reutilizar o circuito para somar palavras binárias de 8, 12, 16, 32, etc.
Neste artigo vamos estudar esse tipo de somador rápido, projeta-lo para somar palavras de 4 bits e descrevê-lo em VHDL.
Somador Carry-Lookahead
Existem três casos de propagação do carry: Kill, Generate e Propagate.
O caso Kill significa que quando as entradas Ai e Bi do somador são iguais a zero, independente do seu carry-in, a propagação do carry-out não existe (“matado”). Isso quer dizer também que o carry-in do próximo estágio vale zero.
O caso Generate significa que quando as entradas Ai e Bi do somador são iguais a um, independente do seu carry-in, a propagação do carry-out existe (“gerado”). Isso quer dizer também que o carry-in do próximo estágio vale um.
O caso Propagate significa que quando as entradas Ai e Bi do somador são iguais a um e zero ou a zero e um respectivamente. Dessa forma o seu carry-in será propagado para o carry-out.
Com essas informações é possível montar uma tabela verdade e assim encontrar uma expressão booleana para o carry-out, ou seja, Ci+1.
*i é um número natural.
Tabela 1: Tabela verdade para o carry-out.
|
|
Ai |
Bi |
Ci+1 |
|
Ki |
0 |
0 |
0 |
|
Pi |
0 |
1 |
Ci |
|
Pi |
1 |
0 |
Ci |
|
Gi |
1 |
1 |
1 |
Para obter a expressão da saída podemos fazer o mesmo procedimento precedente considerando as entradas Ai, Bi e Ci.
Tabela 2: Tabela verdade para a saída.
|
Ci |
Bi |
Ci |
Si |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
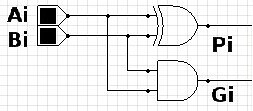
Tendo em vista que os sinais Genarate e Propagate são sempre em função das entradas Ai e Bi, e se comportam como Meio-Somadores (Half-Adders), modelaremos o projeto utilizando-os.
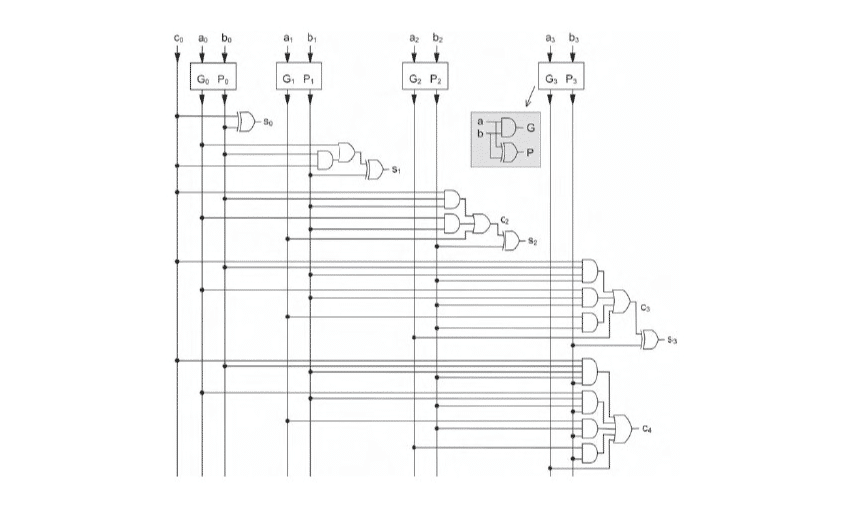
Como nosso objetivo é projetar este somador para palavras de 4 bits, acharemos as equações para cada estágio.
Para o estágio zero, nós temos que o carry-in é uma entrada do circuito, portanto obtemos:
Para o estágio um, temos que o carry calculado no estágio zero será o carry-in desse estágio, isto é:
Seguindo a lógica temos:
Se olharmos para a próxima equação podemos observar que para o próximo estágio (quinto) o número de portas é muito grande, tornando inviável o custo do projeto, além de não se tornar mais rápido em relação a um somador Ripple-Carry por exemplo.
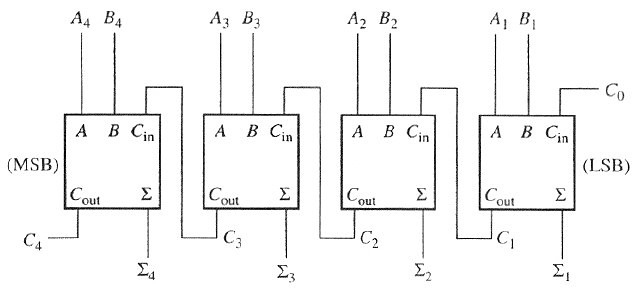
Desempenho do Carry-Lookahead 4 bits em relação ao Ripple-Carry
Comparando a propagação dos carrys-out dos circuitos Ripple-Carry e Carry-Lookahead podemos observar o percusso do carry-out do primeiro somador bem mais longo.
Como no Ripple-Carry é utilizado blocos de somadores completos, temos que cada estágio tem um tempo crítico agregado a 3 portas lógicas. Ou seja, para o circuito completo 12 portas lógicas até o carry-out está bem definido. Diferente do nosso somador estudado que tem tempo crítico agregado a 4 portas lógicas.
Implementação VHDL
Utilizando o software Altera Quartus II 13.0 Web Edition, criou-se o componente HALF_ADDER para ser utilizado no módulo-topo do nosso circuito principal. Esse componente foi descrito como segue:
library IEEE;
use IEEE.std_logic_1164 .all;
entity HALF_ADDER is
port(A, B : in std_logic;
S : out std_logic;
Cout : out std_logic);
end entity;
architecture RTL of HALF_ADDER is
begin
process(A,B)
begin
S <= A xor B;
Cout <= A and B;
end process;
end RTL;
Para o modulo-topo utilizamos o componente HALF_ADDER e escrevemos as equações necessárias para a implementação do somador Carry-Lookahead 4 bits. Onde a descrição utilizada foi:
library IEEE; use IEEE.std_logic_1164 .all; entity CARRYLOOK is port(A, B : in std_logic_vector (3 downto 0); Cin : in std_logic; Cout: out std_logic; S : out std_logic_vector (3 downto 0)); end entity; architecture RTL of CARRYLOOK is signal sig_P : std_logic_vector (3 downto 0); signal sig_G : std_logic_vector (3 downto 0); signal sig_S : std_logic_vector (3 downto 0); signal C1, C2, C3 : std_logic; component HALF_ADDER is port(A, B : in std_logic; S : out std_logic; Cout : out std_logic); end component; begin H0: HALF_ADDER port map (A(0),B(0),sig_P(0),sig_G(0)); H1: HALF_ADDER port map (A(1),B(1),sig_P(1),sig_G(1)); H2: HALF_ADDER port map (A(2),B(2),sig_P(2),sig_G(2)); H3: HALF_ADDER port map (A(3),B(3),sig_P(3),sig_G(3)); C1 <= sig_G(0) or (sig_P(0) and Cin); C2 <= sig_G(1) or (sig_P(1) and sig_G(0)) or (sig_P(1) and sig_P(0) and Cin); C3 <= sig_G(2) or (sig_P(2) and sig_G(1)) or (sig_P(2) and sig_P(1) and sig_G(0)) or (sig_P(2) and sig_P(1) and sig_P(0) and Cin); Cout <= sig_G(3) or (sig_P(3) and sig_G(2)) or (sig_P(3) and sig_P(2) and sig_G(1)) or (sig_P(3) and sig_P(2) and sig_P(1) and sig_G(0)) or (sig_P(3) and sig_P(2) and sig_P(1) and sig_P(0) and Cin); S(0) <= sig_P(0) xor Cin; S(1) <= sig_P(1) xor C1; S(2) <= sig_P(2) xor C2; S(3) <= sig_P(3) xor C3; end RTL;
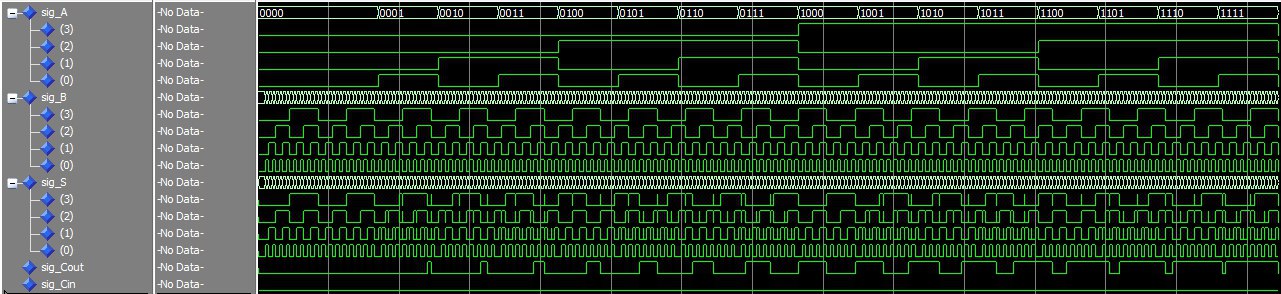
Para verificação do funcionamento foi feito o testbench, abaixo o código e as formas de onda do nosso circuito!
library IEEE; use IEEE.std_logic_1164 .all; use IEEE.std_logic_unsigned .all; entity TB_CARRYLOOK is end TB_CARRYLOOK ; architecture COMPORTAMENTAL of TB_CARRYLOOK is component CARRYLOOK is port(A, B : in std_logic_vector (3 downto 0); Cin : in std_logic; Cout : out std_logic; S : out std_logic_vector (3 downto 0)); end component; signal sig_A : std_logic_vector (3 downto 0) := "0000"; signal sig_B : std_logic_vector (3 downto 0) := "0000"; signal sig_Cin : std_logic := '0'; signal sig_Cout : std_logic; signal sig_S : std_logic_vector (3 downto 0); signal sig_i : std_logic_vector (3 downto 0) := "0000"; signal sig_j : std_logic_vector (3 downto 0) := "0000"; begin U1: CARRYLOOK port map (sig_A,sig_B,sig_Cin,sig_Cout,sig_S); process variable i : integer range 0 to 16; variable j : integer range 0 to 16; constant delay : time := 10 ns; begin for i in 0 to 16 loop sig_A <= sig_i; for j in 0 to 16 loop sig_B <= sig_j; wait for delay; assert sig_A+sig_B = sig_S report "SUM CORRECT" severity error; sig_j <= sig_j + '1'; if( j = 16 ) then sig_i <= sig_i + '1'; end if; end loop; end loop; end process; end COMPORTAMENTAL ;
Veja a forma de onda resultante dos testes.
Para fazer o download de todos os arquivos do projeto para o Quartus, clique no botão abaixo.







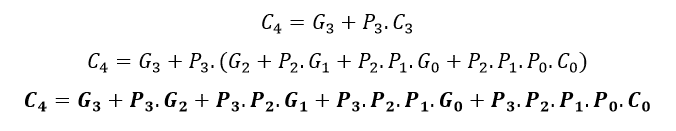


















Cadastrei para fazer download dos arquivos e mostra que não tenho permissão para visualizar o conteudo. Alguma dica?
excelente conteúdo! Me ajudou bastante na prova de eletrônica Digital.. Obrigado por compartilhar tais conhecimentos.