Potência em CA

Até agora a análise de circuitos CA foi focada no cálculo de corrente e tensão. Neste artigo vamos analisar a potência.

O valor mais importante em sistemas de energia elétrica, eletrônicos e de comunicação é a potência. Isso porque envolve a transmissão de energia de um ponto a outro. Assim, todo equipamento elétrico, seja ele de uso residencial ou industrial, tem uma potência nominal responsável por indicar a potência exigida pelo equipamento. É importante dizer que ultrapassar a potência nominal pode causar danos permanentes a um aparelho. 

Nesse artigo, iremos definir a potência instantânea e a potência média. Além de trabalhar os outros conceitos relacionados a potência. 

Potências instantânea e média

Como visto no artigo de Potência, a potência instantânea p(t) absorvida por um componente é o produto da tensão instantânea v(t) no componente e a corrente instantânea i(t) que passa por ele:

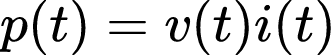
É válido enfatizar que:

A potência instantânea é a potência absorvida por um componente em um dado instante.

Para quantificar a potência instantânea de um circuito CA, iremos considerar um caso geral de uma associação arbitrária de componentes de circuito sob excitação senoidal, em que a tensão e a corrente nos terminais do circuito sejam:

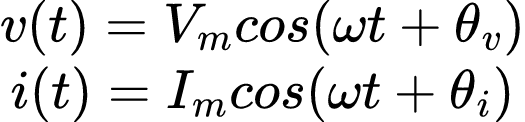
Em que V_m e I_m são as amplitudes (também chamadas de valores de pico) e θ_v e θ_i são, respectivamente, os ângulos de fase da tensão e da corrente. 

Logo, a potência instantânea absorvida pelo circuito é:

Para entender como a potência é absorvida, vamos aplicar a identidade trigonométrica:

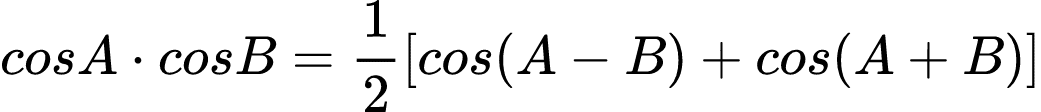
Assim teremos a potência definida como:

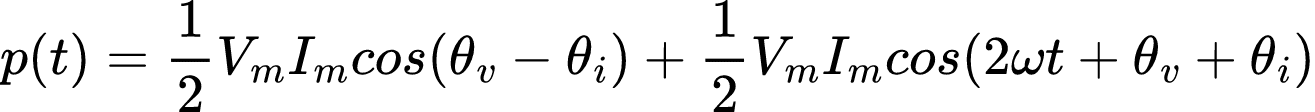
Isso mostra que a potência instantânea é formada por duas partes: uma parte constante (ou seja, independente do tempo) em que seu valor depende da diferença de fase entre a tensão e a corrente, e uma parte com uma função senoidal de frequência 2ω, que é o dobro da frequência angular da tensão ou da corrente.

Por variar com o tempo, a potência instantânea é difícil de ser medida. Então, a potência média é mais conveniente de ser utilizada.

A potência média (watts) é a média da potência instantânea ao longo de um período.

Devido a praticidade, até mesmo o wattímetro, instrumento usado para medir potência, indica a média. Logo, a potência média é dada por:

    Substituindo o p(t) encontrado, temos:

Assim concluímos que devido o primeiro integrando ser uma constante, a sua média será a mesma constante. Já o segundo integrando é uma senoide, a média ao longo do seu período é zero, isso porque a área de uma senoide é ora positiva, ora negativa, então sua área é cancelada zerando o valor. 

Logo, o segundo termo desaparece e a potência média será dada por:

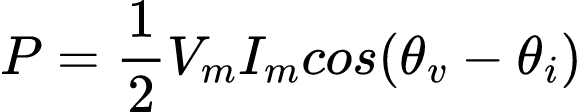
Enquanto p(t) varia com o tempo, P não possui dependência do tempo. Assim, para  encontrar a potência instantânea, devemos ter v(t) e i(t) no domínio do tempo. Já a potência média pode ser encontrada quando a tensão e a corrente estão expressas no domínio do tempo ou no domínio da frequência. 

As formas fasoriais de v(t) e i(t) são:

Utilizando os fasores V e I, escrevemos P como:

Considerando somente a parte real da expressão como a potência média P, temos:

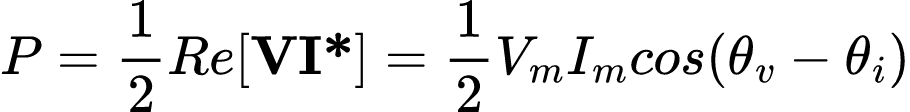
Casos especiais:

• θ_v igual a θ_i

    Quando θ_v = θ_i, significa que a tensão e a corrente estão em fase. Isso configura um circuito puramente resistivo (formado somente por R):

    Em que I²= I ‧ I^*.

    Observando a equação mostra que um circuito puramente resistivo absorve potência o tempo todo. 

• θ_v – θ_i = ±90°

Quando θ_v – θ_i = 90°, temos um circuito puramente reativo:

    A equação mostra que um circuito puramente reativo (ou seja, formado por L ou C) não absorve nenhuma potência média.

Exemplo potência instantânea e média

    Dado v(t) e i(t):

    Determine a potência instantânea e média.

    Começando com a potência instantânea, temos:

    Aplicando a identidade trigonométrica, temos que p é:

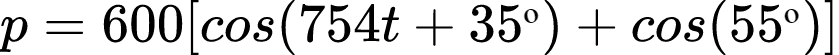
    Já a potência média é:

Máxima transferência de potência média

No artigo Máxima Transferência de Potência, verificamos como maximizar a potência liberada por um circuito resistivo, de tensão CC, com uma carga R_L. Através da equivalência de Thévenin, vimos que seria liberada a potência máxima para a carga se, e somente se, a resistência da carga fosse igual à resistência de Thévenin R_L = R_Th. 

Nos circuitos CA, iremos considerar o circuito da Figura 1 que possui um circuito qualquer conectado a uma carga Z_L, por sua vez este é representado por seu equivalente de Thévenin.

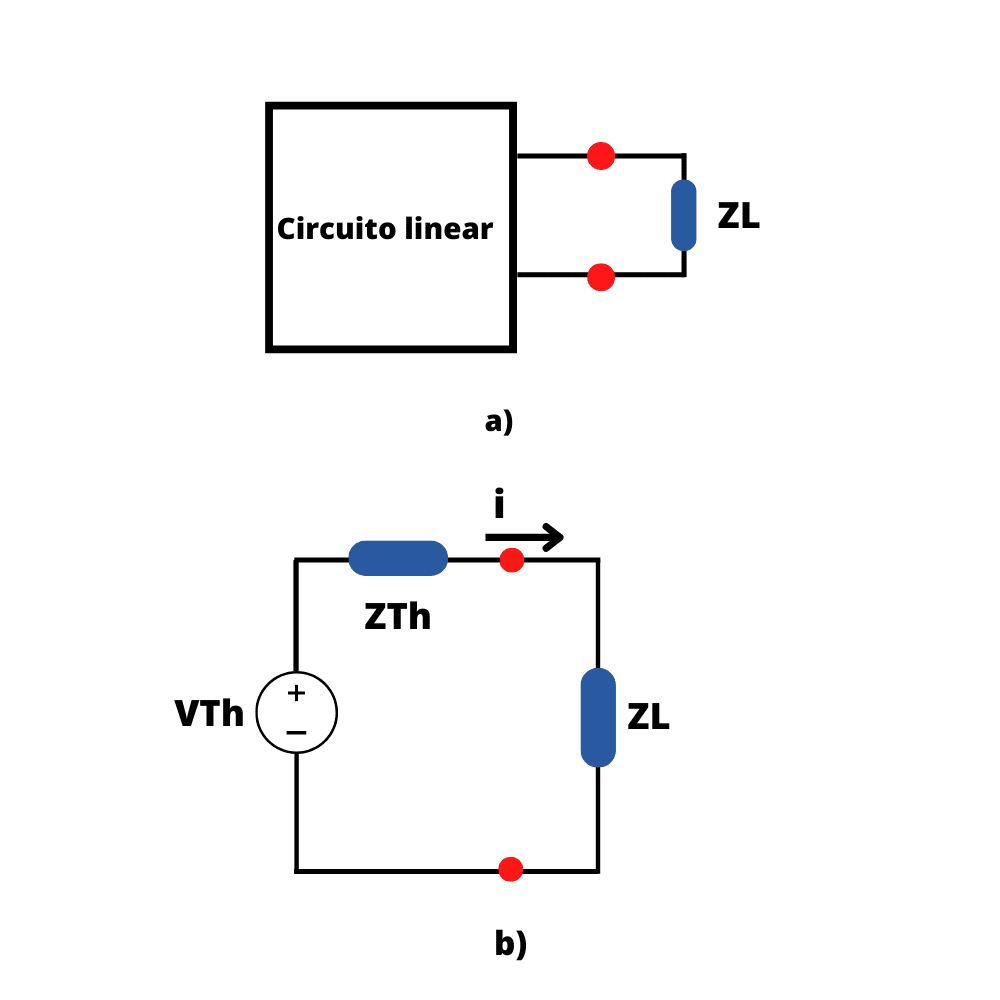
A carga, geralmente, é representada por uma impedância. Então pode ser o modelo um motor elétrico, uma antena, uma TV, etc. Na forma retangular, a impedância de Thévenin Z_Th e a impedância da carga Z_L são, respectivamente:

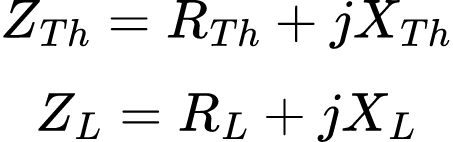
Considerando a Figura 1b, a corrente através da carga é:

Utilizando a equação de potência média, temos:

Para garantir que P seja máxima, precisamos ajustar os parâmetros das cargas R_L e X_L. Para isso, tornamos as derivadas parciais de P em relação a R_L e a X_L igual a zero.

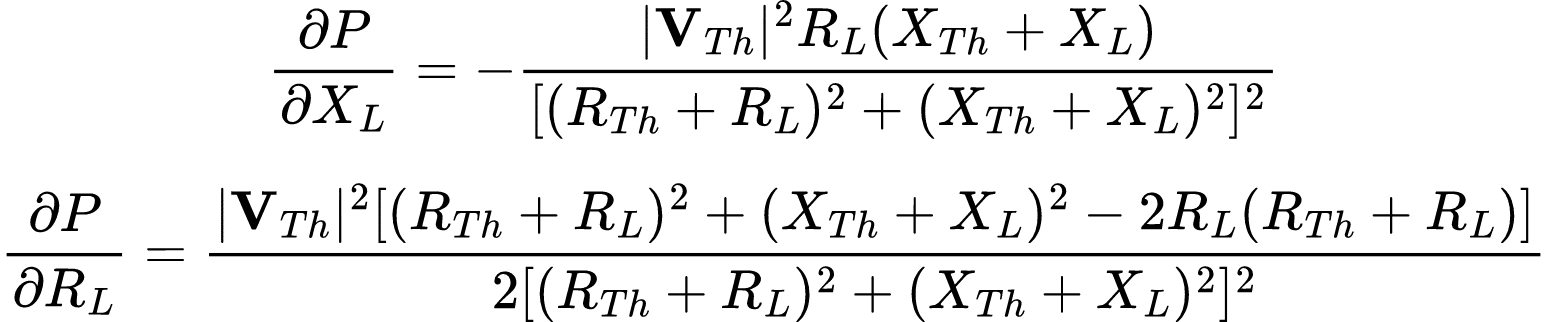
Para que a derivada parcial de P em relação a X_L seja 0, basta:

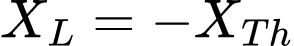
Enquanto que, para a derivada parcial de P em relação a R_L ser 0 é preciso:

Ao combinar ambas as equações, concluímos que para a máxima transferência de potência média, Z_L precisa ser escolhido de forma X_L=–X_Th e R_L = R_Th. Logo:

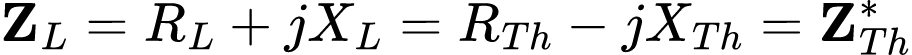
Então:

A máxima transferência de potência média, só é possível se a impedância da carga (Z_L) for igual ao conjugado complexo da impedância de Thévenin  (Z_Th).

Dessa forma, fazendo R_L = R_Th e X_L = –X_Th, na equação da potência média temos o teorema da máxima transferência de potência média:

Em um circuito em que a carga é puramente real, a máxima transferência de potência é obtida considerando X_L = 0:

Isso quer dizer que, a máxima transferência de potência para uma carga resistiva é garantida se a impedância da carga for igual ao módulo da impedância de Thévenin.

Exemplo potência máxima

Vamos determinar a impedância Z_L da carga que maximiza a potência média absorvida do circuito da Figura 2, além de determinar a potência média máxima.

Primeiramente, desenhamos o circuito equivalente de Thévenin nos terminais da carga para obter Z_Th e também V_Th. Começando por Z_Th vamos redesenhar o circuito como:

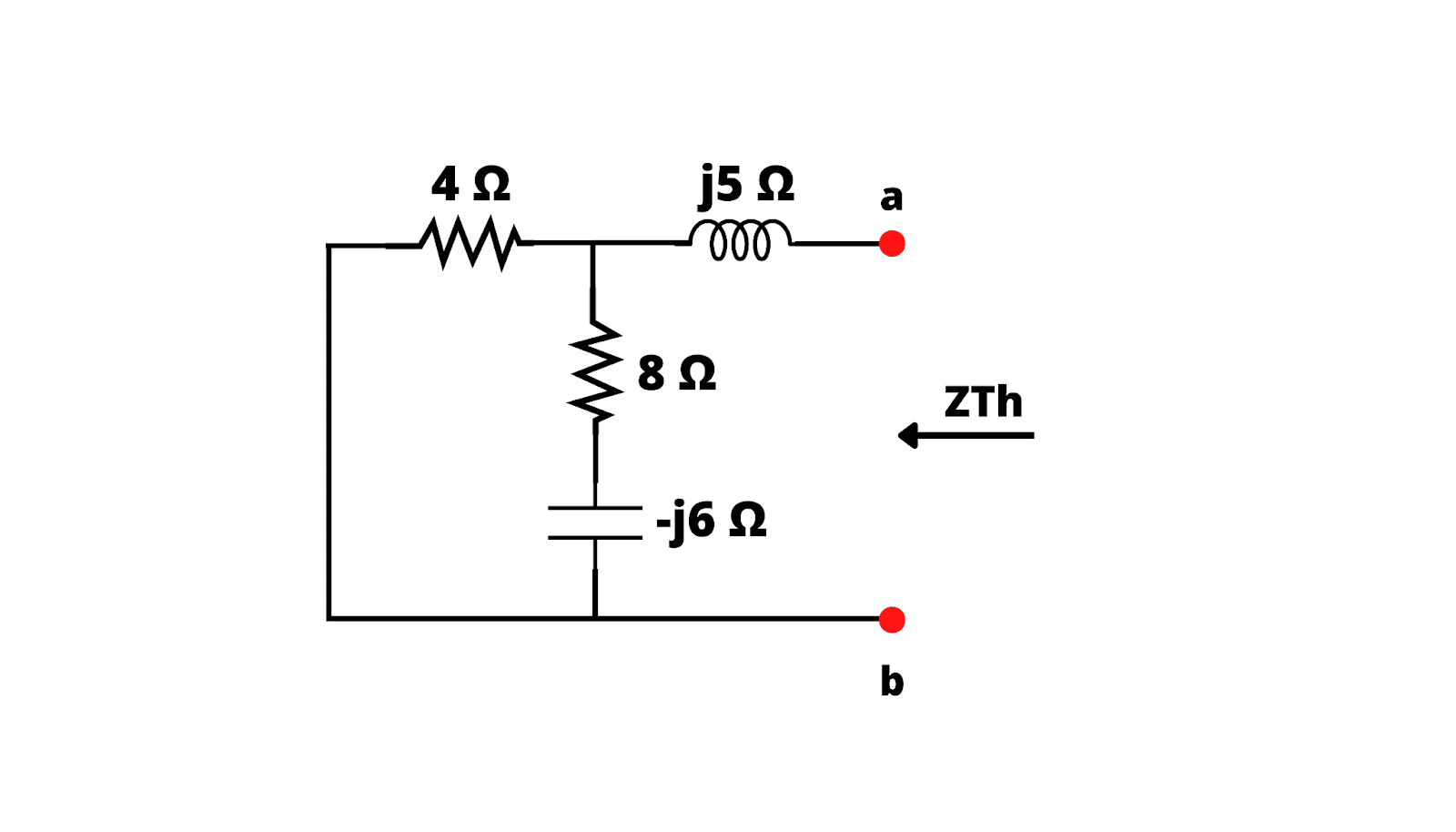
    Assim, temos:

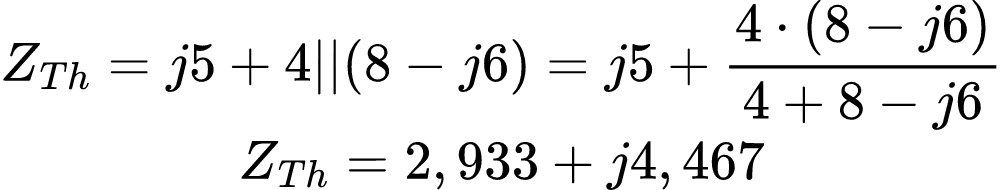
    Para obter Z_L, ou seja, a impedância da carga que absorve a potência máxima, basta pegar o conjugado de Z_Th:

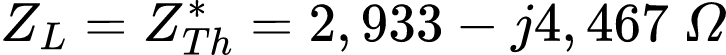
    Para determinar o V_Th, considere o circuito da Figura 4.

    Aplicando divisão de tensão, temos:

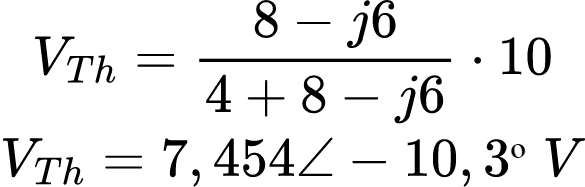
    Por fim, a potência média máxima é:

Referências

ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.