Quando tratamos de circuitos CA, é importante a habilidade de manipular números complexos. Nesse artigo, entenderemos o que são e como trabalhar com eles.

Desenvolvimento

Ao lidar com equações de segundo grau, era comum encontrar a seguinte situação:

No ensino médio diríamos que essa equação não possui solução, mas na verdade ela possui uma solução composta por uma parte imaginária.

Os números reais são os números que já estamos acostumados a lidar na matemática e na física, compostos por todos os números naturais; inteiros; racionais e irracionais. Já os números imaginários são representados através da unidade imaginária, que é definida como:

É comum encontrar a parte imaginária dos números representada tanto por i, como por j. Aqui iremos representar por j, para não confundir com a representação de corrente.

É importante ressaltar que então:

Esse entendimento será importante quando forem realizadas operações matemáticas com números complexos.

Assim, x² pode ser expresso como:

Nesse caso diríamos que esse é um número imaginário puro, isso porque os números complexos são compostos por uma parte real e uma parte imaginária. 

Então, há três formas de representar um número complexo: a retangular; polar e exponencial.

Forma Retangular

Na forma retangular, dizemos que um número complexo z é:

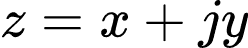
Onde x é a parte real de z, já y é a sua parte imaginária. Ou seja: 

Nesse formato, a parte imaginária sempre estará acompanhada do j.

Forma Polar

A forma polar representa o número complexo z através do seu módulo e o ângulo que ele forma com o eixo real.

Onde, o módulo de z é dado por:

E o ângulo θ com o eixo dependerá dos sinais de x e y, isso porque θ sempre deve ser medido no sentido anti-horário com relação ao eixo real positivo. Então, existem quatro possibilidades para calculá-lo:

Forma retangular	Ângulo θ (forma polar)	Quadrante
		1º quadrante
		2º quadrante
		3º quadrante
		4º quadrante

Pelo cálculo do r e do θ, deu pra perceber que é possível converter da forma retangular para polar, o contrário também é possível. Então, para converter de polar para retangular, basta:

Plano complexo

O plano complexo se parece com o plano xy, mas na realidade, eles são diferentes. No que seria o eixo y, teremos o eixo imaginário, já o eixo x será o eixo real. 

Dessa forma, é possível representar, na forma retangular, o número complexo como um ponto. Na forma polar ele será representado como um vetor, com seu módulo e ângulo representados no plano. Na Figura 1 é possível ver ambas as representações de um número genérico no plano complexo.

Para visualizar melhor vamos considerar duas situações:

1. z₁ = 6 + j8
2. z₂ = 5∠53,13º

Convertendo z₁ da forma retangular para polar, temos:

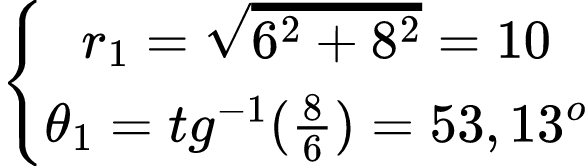
Logo:

Assim, teremos no gráfico:

Convertendo z₂ da forma polar para retangular, temos:

Logo,

Assim, teremos no gráfico:

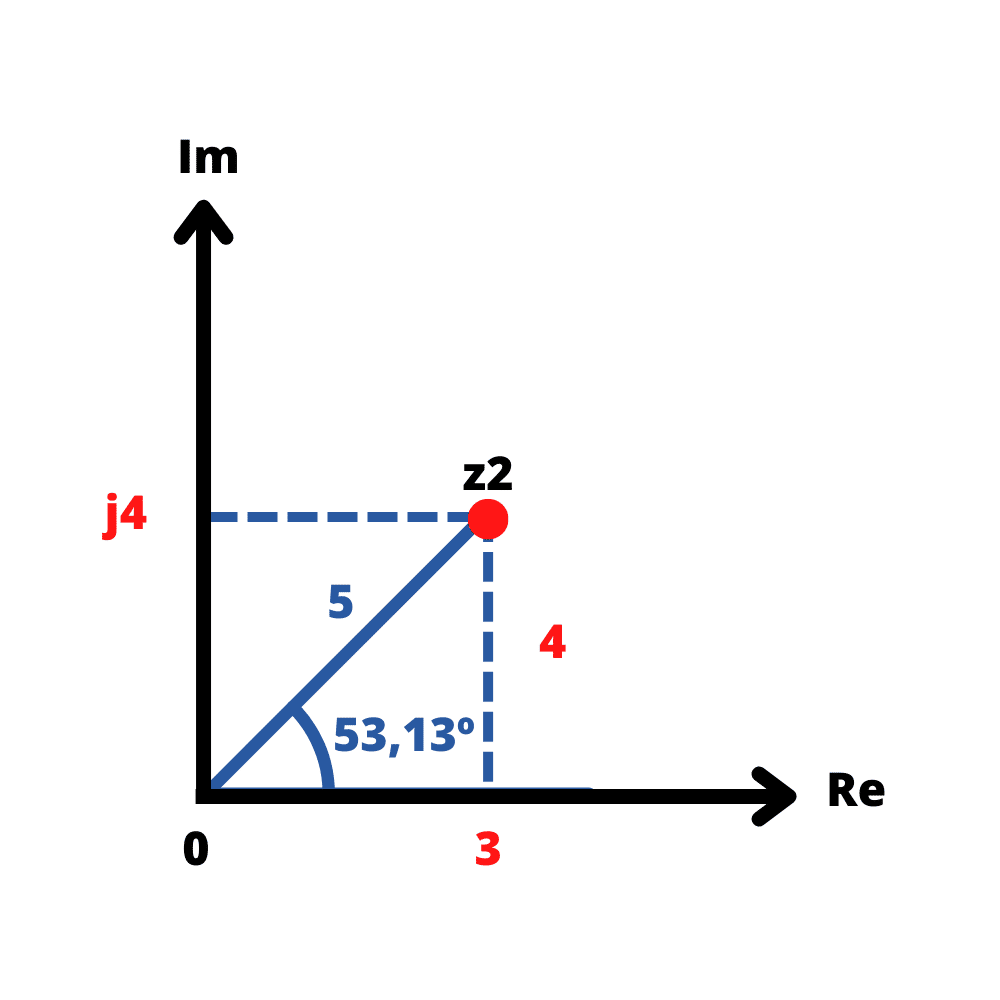
Forma Exponencial

Essa última forma de se representar números complexos, é semelhante a forma polar, pois também utilizamos o mesmo módulo r e o ângulo θ:

Operações Matemáticas com Números Complexos

As operações básicas de adição, subtração, multiplicação e divisão podem ser feitas facilmente com os números complexos. Mas para isso, algumas regras e definições precisam ser enfatizadas.

Primeiramente, números complexos são considerados iguais se suas partes reais e imaginárias forem iguais. Já o conjugado ou complexo conjugado de um número complexo é determinado trocando o sinal da parte imaginária, na forma retangular, ou usando o negativo do ângulo, na forma polar.

Assim, dado o número complexo:

Seu conjugado será:

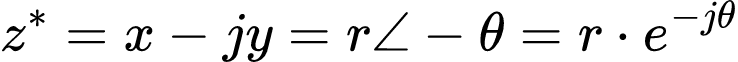
Entendido isso, para somar dois ou mais números complexos, basta somar as partes reais e imaginárias separadamente.

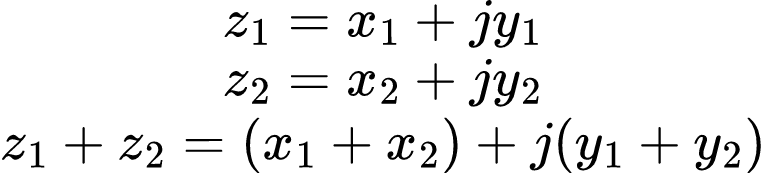
O mesmo vale para a subtração:

Os exemplos de soma e subtração foram dados na forma retangular por ser mais conveniente realizá-las dessa forma. Já o produto e o quociente de dois números complexos são realizados com mais facilidade na forma polar ou exponencial. 

Assim, o produto é feito:

Na forma retangular a operação seria:

Para a divisão na forma polar temos:

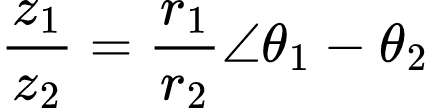
Já na forma retangular é:

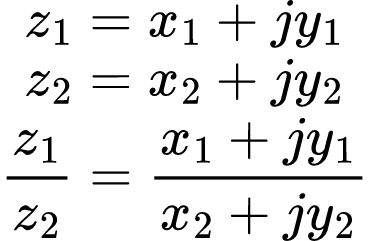
Para que no denominador não tenha parte imaginária, ele é racionalizado multiplicando tanto o numerador, como o denominador por z₂^* (conjugado de z₂).

Exemplos

Para exercitar os conceitos, vamos realizar as operações matemáticas explicadas no tópico anterior. Para isso faremos os dois exemplos:

a) A^*(A + B)

b) (A + B)/(A − B)

Onde:

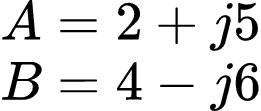
Começando na letra a), a soma de A+B é:

A^* é o conjugado de A, dado por:

Por fim, temos:

Na letra b), começamos realizado A-B:

Por fim, lembrando que é preciso remover a parte imaginária do denominador (usando o conjugado), a divisão é: 

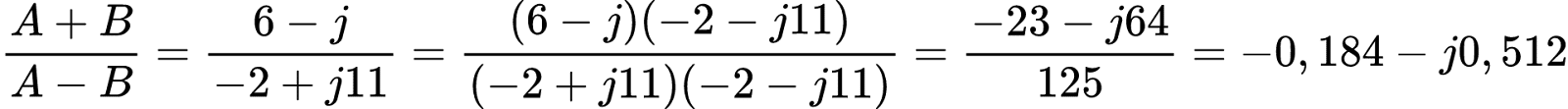
Referências

ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.

BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.