Oi pessoal!!! Nos dois últimos artigos eu falei sobre o Array de uma dimensão. No artigo de hoje falarei sobre o Array de mais de uma dimensão, que também é conhecido como Matriz.
Arrays Bidimensionais
Um Array Bidimensional é um Array com duas posições, configurando-se como uma matriz, ou tabela. Observe a Figura 1:

A Figura 1 apresenta uma Matriz com 3 colunas e 3 linhas. Cada célula dessa matriz correspondente a um elemento, que é indicado por dois índices diferentes: um índice para LINHA e outro índice para a COLUNA. Assim, 1,1 é o elemento da linha 1 com a coluna 1; 2,3 é o elemento da linha 2 com a coluna 3, e assim por diante.
Enquanto o Array Unidimensional tem apenas um índice para acessar e manipular os elementos do vetor, o Array Bidimensional tem dois índices e, por este motivo, precisamos de dois FOR, um dentro do outro, para poder manipular uma matriz. Observe a listagem de código abaixo:
algoritmo "matrizes"
var
linha, coluna: inteiro
m: vetor[1..3,1..3] de real
inicio
para linha de 1 ate 3 faca
para coluna de 1 ate 3 faca
escreva(" Digite um número real para a posição: ", linha, ",", coluna, " : ")
leia (m[linha,coluna])
fimpara
fimpara
escreval("")
para linha de 1 ate 3 faca
para coluna de 1 ate 3 faca
escreval(" | linha: | ", linha, " | coluna: | ", coluna, " | elemento: | ", m[linha, coluna])
fimpara
fimpara
fimalgoritmo
Listagem 1: Populando e Imprimindo uma Matriz 3 x 3

Basicamente a listagem 1 mostra como popular e como imprimir uma matriz e a Figura 2 ilustra como ficaria a Matriz preenchida após a execução do algoritmo. Vamos analisar o código da Listagem 1. A linha 5 declara uma matriz do tipo real:
m: vetor [ 1..3, 1..3 ] de real
É assim que devemos declarar uma matriz. Note que é bem parecida com a declaração do vetor, mas precisamos adicionar uma vírgula e, após a vírgula, colocar a quantidade que queremos de colunas para essa matriz. Assim, se você deseja obter uma matriz com mais de duas dimensões, basta ir separando por vírgulas, mas é preciso tomar muito cuidado com isso. Matrizes com mais de duas dimensões são bem complexas para manipulação.
Para a leitura dos valores digitados pelo usuário, o processo é basicamente o mesmo do Vetor. Entretanto, note que agora devemos colocar os dois índices na leitura, um para a linha e outro para a coluna:
leia ( m [ linha , coluna ] )
Optei por usar os nomes dos índices como linha e coluna para ficar mais fácil, entretanto, vocês normalmente encontrarão os nomes “i” e “j” nas bibliografias e materiais disponíveis na Internet.
Agora note, as linhas de 9 a 14 correspondem ao código para popular a Matriz. Existem dois FOR, um dentro do outro. Sim! É assim mesmo que devemos fazer, não daria certo popular uma matriz se os FOR fossem independentes, dessa forma teríamos dois vetores e não uma matriz. O preenchimento da Matriz ocorre da esquerda para a direita e de cima para baixo, por isso, primeiro é preenchida a linha e depois a coluna, basicamente como ilustra a Figura 3:
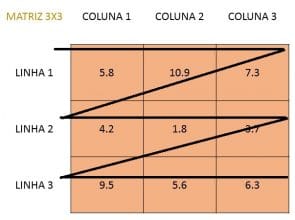
Vamos entender melhor fazendo o teste de mesa do código que é apresentado na Tabela 1.
| iteração | linha de 1 até 3 | coluna de 1 até 3 | m [ linha , coluna] |
| 1 | 1 | 1 | m[1,1] = 5.8 |
| 2 | 1 | 2 | m[1,2] = 10.9 |
| 3 | 1 | 3 | m[1,3] = 7.3 |
| 4 | 2 | 1 | m[2,1] = 4.2 |
| 5 | 2 | 2 | m[2,2] = 1.8 |
| 6 | 2 | 3 | m[2,3] = 3.7 |
| 7 | 3 | 1 | m[3,1] = 9.5 |
| 8 | 3 | 2 | m[3,2] = 5.6 |
| 9 | 3 | 3 | m[3,3] = 6.3 |
Tabela 1: Teste de Mesa da Listagem 1
Observe que, ao entrar no primeiro FOR, o mesmo fica travado até que o FOR subsequente termine sua execução, então, somente quando o FOR da coluna atingir o valor 3, é que ele sai desse FOR mais interno e volta para o FOR mais externo. Voltando ao FOR externo, ele será incrementado de um, passando então para a linha 2 e entrando novamente no FOR mais interno que, novamente, será executado de 1 até que a coluna atinja o valor 3.
Acessando, modificando e imprimindo um elemento específico da matriz
Se desejar trabalhar especificamente com um elemento da matriz, você pode fazê-lo. Observe a listagem 2 de código.
algoritmo "matrizes"
var
linha, coluna: inteiro
m: vetor[1..3,1..3] de real
inicio
para linha de 1 ate 3 faca
para coluna de 1 ate 3 faca
m[linha,coluna] <- 0.0
fimpara
fimpara
escreval("")
para linha de 1 ate 3 faca
para coluna de 1 ate 3 faca
escreval(" | linha: | ", linha, " | coluna: | ", coluna, " | elemento: | ", m[linha, coluna])
fimpara
fimpara
m[1,1] <- 3.9
m[3,3] <- 0.7
escreval("")
escreval("Novo valor de m[1,1]", m[1,1])
escreval("Novo valor de m[3,3]", m[3,3])
fimalgoritmo
Listagem 2: Imprimindo e modificando posições específicas da matriz.
Como você pode notar, as linhas 23 e 24 modificam os valores originais das posições 1,1 e 3,3. As linhas 27 e 28 imprimem no console os novos valores dessas posições. Neste código, também inicializo a matriz atribuindo o valor zero a todas as posições da matriz, conforme mostra as linhas de 9 a 13.
Finalizando
Assim como em Vetores, você também pode realizar operações com os elementos das matrizes, como copiar os valores de uma matriz para um vetor ou outra matriz, realizar operações entre matrizes (como na matemática), realizar buscas, etc. Linguagens orientadas a objetos normalmente fornecem métodos específicos para trabalhar com matrizes, o que facilita, e muito, a implementação do código. Por isso, não se esqueça de sempre verificar os recursos que a Linguagem lhe fornece. Vamos ver como Matrizes são definidas, declaradas e manipuladas em outras linguagens de programação.
C
#include <stdio.h>
int main()
{
int mat[2][2], i, j;
for (i=0; i<2; i++)
{
for (j=0; j<2; j++)
{
mat[i][j] = 0;
}
}
printf("\n");
for (i=0; i<2; i++)
{
for (j=0; j<2; j++)
{
printf("%d \n", mat[i][j]);
}
}
printf("\n");
for (i=0; i<2; i++)
{
for (j=0; j<2; j++)
{
printf("\n Digite o elemento da linha %d e coluna %d: ", i, j);
scanf("%d%*c ", &mat[i][j]);
}
}
printf("\n");
for (i=0; i<2; i++)
{
for (j=0; j<2; j++)
{
printf("%d \n", mat[i][j]);
}
}
printf("\n");
getchar();
return 0;
}
JAVA
package vetores;
import java.util.Scanner;
public class matrizes {
public static void main(String[] args) {
int i, j;
double[][] m = new double[3][3];
Scanner s = new Scanner(System.in);
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
System.out.println(" Digite um número real: ");
m[i][j] = s.nextDouble();
}
}
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
System.out.println(" | linha: " + i + " | coluna: " + j + " | Matriz: " + m[i][j]);
}
}
}
}
PASCAL
PROGRAM matrizes;
USES wincrt, CRT;
VAR
mat: ARRAY[1..2, 1..2] OF INTEGER;
i, j: INTEGER;
BEGIN
CLRSCR;
writeln('');
FOR i:=1 TO 3 DO
BEGIN
FOR j:=1 TO 3 DO
BEGIN
mat[i,j] := 0;
END;
END;
writeln('');
FOR i:=1 TO 3 DO
BEGIN
FOR j:=1 TO 3 DO
BEGIN
WRITE ('Digite o elemento da linha ', i, ' e coluna ', j, ' ');
READLN(mat[i,j]);
END;
END;
writeln('');
FOR i:=1 TO 3 DO
BEGIN
FOR j:=1 TO 3 DO
BEGIN
WRITELN (' | Linha: ', i, ' | Coluna: ', j, ' | Elemento: ', mat[i,j]);
END;
END;
writeln('');
READLN;
END.
Exercícios
1. Crie um programa que preencha uma matriz 5 X 5 com números inteiros, calcule e mostre a soma: a) dos elementos da linha 4; b) dos elementos da coluna 2; c) dos elementos da diagonal principal; d) dos elementos da diagonal secundária; e) de todos os elementos da matriz.
2. Crie um programa que: a) receba o preço de dez produtos e armazene-os em um vetor; b) receba a quantidade estocada de cada um desses produtos, em cinco armazéns diferentes, utilizando uma matriz 5 X 10. O programa deverá calcular e mostrar: a) a quantidade de produtos estocados em cada um dos armazéns; b) a quantidade de cada um dos produtos estocados, em todos os armazéns juntos; c) o preço do produto que possui maior estoque em um único armazém; d) o menor estoque armazenado; d) o custo de cada armazém.
3. Elabore um programa que preencha uma matriz 12 X 4 com os valores das vendas de uma loja, em que cada linha representa um mês do ano e cada coluna representa uma semana do mês. O programa deverá calcular e mostrar: a) o total vendido em cada mês; b) o total vendido em cada semana durante todo o ano; c) o total vendido pela loja no ano.
4. Elabore um programa que: preencha uma matriz 6 X 4, recalcule a matriz digitada onde cada linha deverá ser multiplicada pelo maior elemento da linha em questão. Mostre a matriz resultante.

















Você teria a resposta da 3 em C?
Oi Ariane. Eu acho que postei as respostas destes exercícios na série de algoritmos. Precisa dar uma conferida lá pois não tenho certeza.Obrigada
Elabore um programa que preencha uma matriz 12 X 4 com os valores das vendas de uma loja, em que cada linha representa um mês do ano e cada coluna representa uma semana do mês. O programa deverá calcular e mostrar: a) o total vendido em cada mês; b) o total vendido em cada semana durante todo o ano; c) o total vendido pela loja no ano. Consegui a solução, mas preciso de uma com menos de 1.000 caracteres. Pode me ajudar?
Oi André, obrigada pelo seu comentário e desculpe pela demora pra responder. Ando bem ocupada com o doutorado. Pq precisa limitar a 1000 caracteres?
Oi, alguém conseguiu fazer o exercício 02? Eu não estou conseguindo totalizar por armazém… sai o total de tudo. Segue meu codigo. #include #include #include int main() { setlocale(LC_ALL,”portuguese”); float precco[10]; int estoque[5][10]; int menor = 999999; int maior = 0; int maior_estoque = 0; int i, j; int soma[5] = {0}; int somatotal = 0; printf(“6) Faça um programa que receba o preço de 10 produtos e armazene-os em um vetor, receba a quantidade estocada de cada um destes produtos em 5 armazéns diferentes utilizando uma matriz 5 X 10. Depois calcule e mostre:\n\n a quantidade de produtos estocados… Leia mais »
Oi, estou preparando um artigo com as soluções tá bom! Obrigada
oi, conseguiu a resposta dessa pergunta???????????