ÍNDICE DE CONTEÚDO
- Arquitetura de Conjunto de Instruções MIPS
- Primeira Instrução MIPS
- Compilação de Expressões no MIPS
- Convertendo uma instrução com Array no MIPS
- Armazenando um valor em Array no MIPS
- Instruções LW e SW com Array no MIPS
- Instrução IF Simples no MIPS
- Instrução IF Composto no MIPS
- Instrução SLT no MIPS
- Operações Lógicas no MIPS
- Operação Lógica AND no MIPS
- Operação Lógica OR no MIPS
- Operação Lógica NOT no MIPS
- Endereços de Memória no MIPS
- Operandos Imediatos e Constantes no MIPS
- Compilando Arrays com índice variável no MIPS
- Testando as instruções MIPS no MARS
- Executando um Array no MARS para MIPS
- Sinal e Overflow no MIPS
- Compilando instruções com ou sem Sinal, Overflow e Imediato no MIPS
- Compilando While no MIPS
- Compilando Switch/Case no MIPS
- Compilando Funções e Procedimentos no MIPS
- Compilando Procedimentos Recursivos e Aninhados no MIPS
- Detalhamento da Compilação de Procedimentos no MIPS
- MIPS: Instruções de Multiplicação
- MIPS: Instruções de Divisão
- MIPS: Subtração e outras instruções
- Compilando o comando FOR no MIPS
- Ponto Flutuante no MIPS
- Convertendo Código de Máquina em Assembly MIPS – Parte 1
- MIPS: Resolução dos exercícios – Parte 1
- MIPS: Resolução de Exercícios Parte 2
Oi pessoal! Tudo bem? No último artigo eu falei sobre o SINAL dos números e também sobre o OVERFLOW. Hoje vou apresentar a vocês algumas instruções que foram projetadas para lidar com isso. Vamos começar então?
Adição com Overflow – ADD
Esta operação aritmética nós já aprendermos, lá no terceiro artigo!
Adição sem Overflow – ADDU
Esta operação aritmética funciona praticamente da mesma forma que a Adição com Overflow, porém esta instrução não retém o overflow e, apenas a título de curiosidade, ADDU significa ADD Unsigned Word, isto é, traduzindo literalmente: Adição de Palavras Sem sinal. Esta operação é para módulos aritméticos de 32 bits que não são retidos no overflow, sendo apropriada para aritmética sem sinal, como a aritmética de endereços ou ambientes aritméticos inteiros que ignoram o overflow, como acontece na aritmética da linguagem C.
ADDU rd, rs, rt # rd = rs + rt
Exemplo:
ADDU $s0, $s1, $s2 # s0 = s1 + s2
Onde rd é o registrador destino, rs é o primeiro operando e rt é o segundo operando. O formato é o seguinte:
|
opcode |
rs |
rt |
rd |
shamt |
funct |
|
0 |
|
|
|
0 |
(33)2 ou (0x21)16 |
|
6 bits |
5 bits |
5 bits |
5 bits |
5 bits |
6 bits |
Exemplo:
|
opcode |
rs |
rt |
rd |
shamt |
funct |
|
0 |
$s1 |
$s2 |
$s0 |
0 |
33 |
|
0 |
17 |
18 |
16 |
0 |
33 |
|
000000 |
10001 |
10010 |
10000 |
00000 |
100001 |
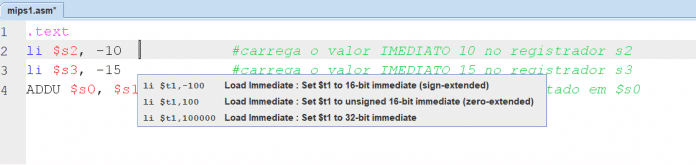
Para testarmos essa instrução no Mars, devemos, antes de qualquer coisa, carregar valores para os registradores temporários e depois realizar a soma. Algo interessante a se falar aqui é que, ao usar o LI, o MARS mostra uma mensagem, explicando o tipo de imediato que será carregado de acordo com o imediato que você digitou, veja:
Traduzindo as mensagens (ao pé da letra praticamente):
li $t1, -100 define $t1 como um imediato de 16 bits com sinal estendido
li $t1, 100 define $t1 como um imediato de 16 bits sem sinal com zero estendido
li $t1, 10000 define $t1 como um imediato de 32 bits
Zero-extended, ou zero estendido, significa que os bits “não utilizados” de ordem mais alta são zeros. Bem, vamos testar então o nosso código com os seguintes valores:
|
$s1 |
$s2 |
$s0 |
|
-10 |
-15 |
(-10) + (-15) = -25 |
|
-10 |
+15 |
(-10) + (+15) = +5 |
|
+10 |
-15 |
(+10) + (-15) = -5 |
|
+10 |
+15 |
(+10) + (+15) = +25 |
|
-100 |
-150 |
(-100) + (-150) = -250 |
|
-100 |
+150 |
(-100) + (+150) = +50 |
|
+100 |
-150 |
(+100) + (-150) = -50 |
|
+100 |
+150 |
(+100) + (+150) = +250 |
|
-1.000 |
-1.500 |
(-1.000) + (-1.500) = -2.500 |
|
-1.000 |
+1.500 |
(-1.000) + (+1.500) = +500 |
|
+1.000 |
-1.500 |
(+1.000) + (-1.500) = -500 |
|
+1.000 |
+1.500 |
(+1.000) + (+1.500) = +2.500 |
|
-10.000 |
-15.000 |
(-10.000) + (-15.000) = -25.000 |
|
-10.000 |
+15.000 |
(-10.000) + (+15.000) = +5.000 |
|
-10.000 |
-15.000 |
(+10.000) + (-15.000) = -25.000 |
|
-10.000 |
+15.000 |
(+10.000) + (+15.000) = +5.000 |
Você fará o teste manualmente ok, nada de fazer um Array pra ir mais rápido, pois a intenção aqui é que você analise o que está acontecendo. Seguindo o código abaixo, você substituirá os valores em $s0 e $s1 conforme a tabela e a cada par de valores, vai executar o arquivo .asm, verificando os valores em hexadecimais e os estados dos registradores. Você vai perceber que quando o número é negativo (-), o “número” hexadecimal correspondente será F e, quando o número for positivo (+), zeros serão adicionados à esquerda.
|
1 2 3 4 |
.text li $s1, -10 #carrega o valor IMEDIATO -10 no registrador s1 li $s2, +15 #carrega o valor IMEDIATO +15 no registrador s2 ADDU $s0, $s1, $s2 #soma $s1 com $s2 e armazena o resultado em $s0 |
Adição com Imediato e com Overflow – ADDI
Esta instrução já foi estudada no 15.º artigo
Adição com Imediato e sem Overflow – ADDIU
Esta operação aritmética funciona praticamente da mesma forma que a Adição com Imediato e com Overflow, e significa Add Immediate Unsigned Word, ou Adição Imediata de Palavras sem Sinal. Esta operação é para módulos aritméticos de 32 bits que não são retidos no overflow, sendo apropriada para aritmética sem sinal, como na aritmética de endereços ou ambientes aritméticos inteiros que ignoram o overflow, como a aritmética da linguagem C.
ADDIU rt, rs, imm # rt = rs + imm
Exemplo:
ADDIU $s0, $s1, 20 # s0 = s1 + 20
Onde rd é o registrador destino, rs é o primeiro operando e rt é o segundo operando. O formato é o seguinte:
|
opcode |
rs |
rt |
imm |
|
9 |
|
|
|
|
6 bits |
5 bits |
5 bits |
16 bits |
Exemplo:
|
opcode |
rs |
rt |
imm |
|
9 |
16 |
17 |
20 |
|
001001 |
10000 |
10001 |
0000 0000 0001 0100 |
No Mars ficará da seguinte forma:
|
1 2 3 |
.text li $s1, -10000 #carrega o valor IMEDIATO no registrador s1 ADDIU $s0, $s1, 15000 #soma $s1 com $s2 e armazena o resultado em $s0 |
Mais uma vez aconselho a fazer o teste para a Tabela de valores apresentada em ADDU.
Subtração com Overflow – SUB
Esta operação aritmética nós já aprendermos, lá no terceiro artigo!
Subtração sem Overflow – SUBU
Esta operação aritmética funciona praticamente da mesma forma que a Subtração com Overflow, e significa Subtract Unsigned Word, ou Subtração de Palavras sem Sinal. Esta operação é para módulos aritméticos de 32 bits que não são retidos no overflow, sendo apropriada para aritmética sem sinal, como na aritmética de endereços ou ambientes aritméticos inteiros que ignoram o overflow, como a aritmética da linguagem C.
SUBU rt, rs, rt # rt = rs + rt
Exemplo:
SUBU $s0, $s1, $s2 # s0 = s1 + s2
Onde rd é o registrador destino, rs é o primeiro operando e rt é o segundo operando. O formato é o seguinte:
|
opcode |
rs |
rt |
rd |
shamt |
funct |
|
0 |
|
|
|
0 |
(35)2 ou (0x23)16 |
|
6 bits |
5 bits |
5 bits |
5 bits |
5 bits |
6 bits |
Exemplo:
|
opcode |
rs |
rt |
rd |
shamt |
funct |
|
0 |
$s1 |
$s2 |
$s0 |
0 |
35 |
|
0 |
17 |
18 |
16 |
0 |
35 |
|
000000 |
10001 |
10010 |
10000 |
00000 |
100011 |
No Mars ficará da seguinte forma:
|
1 2 3 4 |
.text li $s1, -10000 li $s2, +15000 SUBU $s0, $s1, $s2 |
Conclusão
Como vocês puderam ver, as instruções se comportam praticamente da mesma forma. Tendo como base estes exemplos, vocês já serão capazes de entender o funcionamento das outras. Como sugestão para aprofundar seus estudos, acesse o site do MIPS Technologies, baixe todo o material correspondente a MIPS32bits e dê uma olhada na descrição das instruções. A propósito, muito do que temos estudado nesta série tem como fonte esses documentos, inclusive este artigo! É isso pessoal, bons estudos e até o próximo artigo.
Saiba mais
Entendendo a Aritmética em Ponto Fixo
Utilizando o ULP do ESP32 para co-processamento
Tipos de dados para uso em algoritmos
Atuo como Professora de Informática e Computação desde 2001, atendendo de forma especial a Terceira Idade e Concurseiros. Desde 2009 venho atuando como Docente no Ensino Superior em diversos cursos de Graduação e Pós Graduação Lato Sensu, tanto presenciais, quanto semipresenciais e à distância. Ministrei várias disciplinas onde ensino os estudantes a desenvolverem plataformas e sistemas computacionais. Orientei vários trabalhos acadêmicos, desenvolvi inúmeros materiais, trabalhei com pesquisa, ensino, extensão e inovação, ministrei palestras em vários eventos. Mais recentemente venho ofertando serviços na área de tecnologia como desenvolvimento de sistemas, treinamentos, consultoria, mentoria, etc. Comecei meu Doutorado na área de Machine Learning (Multi-label Classification) na UFSCar em 02/2019 e devo terminar em 01/2023. Também estudo canto, jogo vôlei, sou geek, nerd, otaku e gamer!
