Nos circuitos com fontes CA, analisaremos o comportamento da entrada senoidal através de fasores. Então, os componentes que compõem o circuito – resistores, capacitores e indutores – também precisarão apresentar relações entre tensão e corrente elétrica descrita por números complexos. Estes são chamados de impedância e admitância.
Neste artigo, estudaremos os comportamentos da impedância e admitância de cada um dos elementos passivos citados.
Impedância
Relembrando o artigo sobre fasores, determinamos as relações tensão-corrente para três elementos (resistor R, indutor L e capacitor C), como:
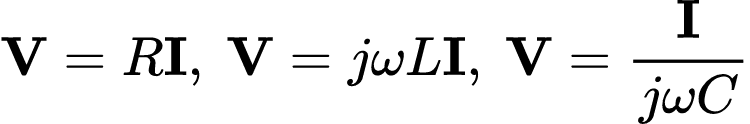
Para obter a Lei de Ohm na forma fasorial, vamos começar escrevendo essas equações em razão da tensão fasorial e a corrente fasorial:

Assim, concluímos que a Lei de Ohm para fasores é:
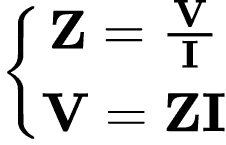
Em que Z é um valor que depende da frequência sendo chamado de impedância, cuja unidade é Ohms (Ω).
Assim, as impedâncias de resistores, indutores e capacitores são as mostradas na Tabela 1.
| Elemento | Impedância |
| R | Z=R |
| L | Z=jωL |
| C | Z=1/jωC |
Podemos observar na tabela que a impedância do indutor e do capacitor são, respectivamente, ZL = jωL e ZC = –j/ωC. Ao considerar dois casos extremos de frequência angular, teremos:

Onde, ω=0 significa um circuito com fontes CC. Nesse caso temos o comportamento já estudado: o indutor atua como um curto-circuito, já o capacitor opera como um circuito aberto.

Onde, ω=∞ significa um circuito com alta frequência C. Nesse caso temos que, em alta frequência, o indutor é um circuito aberto e o capacitor é um curto-circuito.
Por ser um valor complexo, a impedância pode ser expressa na forma retangular:
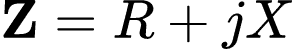
Em que R é a resistência e a parte real de Z, enquanto que X é a reatância e a parte imaginária de Z. A reatância pode ser positiva ou negativa, se for positiva chamamos a impedância de indutiva, se for negativa chamamos de capacitiva.
O fator determinante para ser do tipo indutiva ou capacitiva é a frequência aplicada. Isso acontece, pois em frequências baixas, os elementos capacitivos (de maneira geral) fornecem a maior contribuição para a impedância total, já em frequências altas, os elementos indutivos são os responsáveis pela maior contribuição para a impedância total. Isso pode ser observado na análise do comportamento dos elementos para ω=0 e ω=∞ feito anteriormente.
A impedância também pode ser escrita na forma polar:

É importante entender alguns pontos sobre a impedância:
- É uma quantidade que representa a oposição do circuito ao fluxo de corrente senoidal;
- Por mais que seja a razão entre dois fasores, a impedância não é um fasor. Isso porque não corresponde a um valor que se comporta como uma senóide (que varia com o tempo), mas com uma grandeza fixa.
Admitância
Em algumas situações é mais conveniente trabalhar com a admitância.
A admitância é o inverso da impedância e é medida em Siemens (S).
Assim, a admitância Y de um circuito é a razão entre a corrente fasorial e a tensão fasorial do circuito.

Então as admitâncias de resistores, indutores e capacitores são as mostradas na Tabela 2.
| Elemento | Admitância |
| R | Y=1/R |
| L | Y=1/jωL |
| C | Y=jωC |
Por ser um valor complexo, a admitância pode ser expressa na forma retangular:

Em que G é a condutância e a parte real de Y e B é a susceptância e parte imaginária de Y. Tanto admitância, condutância e susceptância são expressas na unidade Siemens (ou mhos).
Para determinar o valor da condutância e susceptância, consideramos:

Racionalizando a parte imaginária:
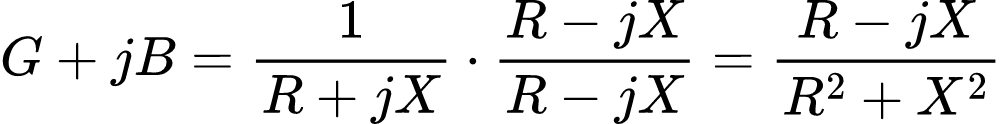
Separando a parte real da imaginária, temos:
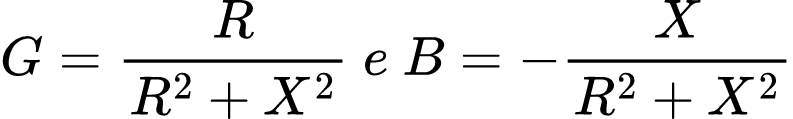
Dessa forma, observamos que G=1/R somente se X=0.
Resumo
Em resumo a impedância e admitância dos elementos passivos de circuitos são os mostrados na Tabela 3.
Tabela 3 – Impedância e admitância de elementos passivos.
| Elemento | Impedância | Admitância |
| R | Z=R | Y=1/R |
| L | Z=jωL | Y=1/jωL |
| C | Z=1/jωC | Y=jωC |
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.

















Muito bom. Parabéns!