Para realizar o controle do sistema de injeção de combustível, foi utilizado o algoritmo que segue os modelos físicos propostos por Elbert Hendricks (HENDRICKS, 1997). O modelo simplificado da dinâmica do fluxo de injeção de combustível, proposto por Hendricks, mantém o controle do fluxo de combustível (em vez da massa de combustível) no coletor de admissão e pode ser facilmente adaptado para outros motores.
Nesse algoritmo, é utilizada a equação dos gases ideais para aproximar a relação entre a densidade do ar, a pressão do ar e a temperatura do ar no coletor de admissão. Baseando-se na equação 1, é possível deduzir que a densidade do ar admitido é proporcional à pressão absoluta do ar dentro do coletor de admissão e inversamente proporcional à temperatura do ar.
Onde:

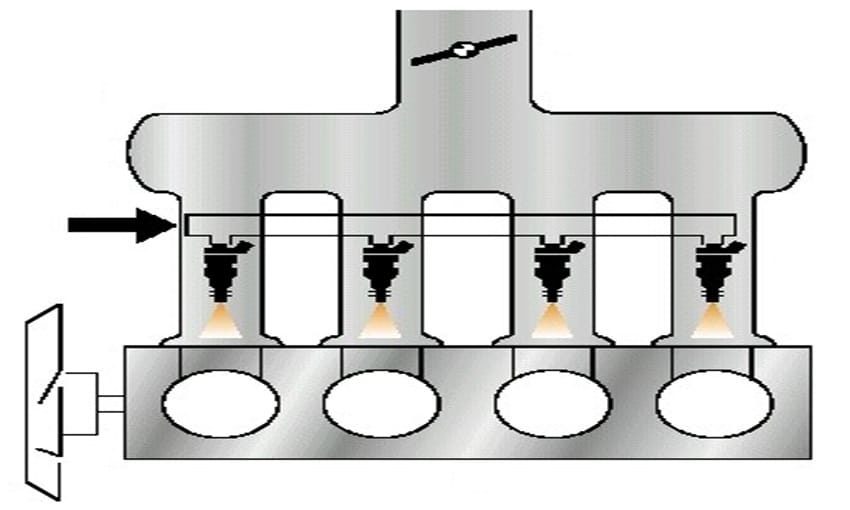
Desta mesma equação, é possível determinar a massa de combustível necessária para o regime de operação do motor. Nos motores equipados com injeção eletrônica de combustível, esta massa de combustível é inserida para dentro de cada cilindro quando as válvulas injetoras de combustível são abertas pela unidade controladora. Diferentes motores possuem diferentes números de cilindros e diferentes números de injetores. Levando isto em conta e tendo em mente que o único parâmetro de controle da ECU é o tempo que a válvula injetora permanece aberta, a equação 2 relaciona a massa de combustível com o número de injetores e cilindros, além de considerar o fluxo de combustível da válvula injetora, que é um parâmetro físico de construção de cada válvula injetora e não há como ser alterado.
Substituindo a equação 2 na equação 1, é possível chegar à equação que determina o tempo de injeção em função da massa de combustível seguindo a estratégia speedy-density.
Onde:

Quase todos os parâmetros desta equação são constantes e dependem de fatores construtivos do motor. Os únicos parâmetros que variam de acordo com o estado atual do motor são a pressão absoluta do ar admitido, a temperatura do ar admitido e a eficiência volumétrica. A eficiência volumétrica é definida como a massa de mistura ambiente que entra no cilindro no tempo de admissão dividida pela massa de mistura que vai preencher o espaço disponível na câmara, considerando-se a densidade do ar na admissão. A eficiência volumétrica pode ser expressa como:
Onde:

Em motores de combustão interna ciclo Otto, o efeito desejado é o aumento da eficiência volumétrica. Ela tem um efeito direto na potência de saída do motor, na medida em que a massa de ar no cilindro determina a quantidade de combustível que pode ser injetada num determinado instante de operação do motor. A melhor seleção dos tempos de abertura e fechamento das válvulas de admissão e escape de cada projeto é fundamental para maximizar-se a eficiência volumétrica. Para rotações inferiores a 2000 RPM, observa-se que menores ângulos de fechamento da válvula melhoram a eficiência volumétrica. No entanto, conforme a faixa de rotação aumenta, o atraso no fechamento da válvula de admissão melhora a relação da eficiência volumétrica. Se desejar conhecer mais sobre o controle eletrônico de válvulas de um motor ciclo Otto verifique o artigo completo “aqui”.
Para implementar o controle da injeção de combustível, todas as equações anteriores devem ser consideradas. Um exemplo de software para implementação desse controle é apresentado abaixo, onde foi desenvolvida uma função do cálculo do tempo de injeção.
void CalculoTempoInjecao(uint8_t *Tinj) {
float Ev = 0; //Variavel p/ calculo da eficiencia volumetrica
uint16_t Tus = 0; //Variavel p/ calculo do tempo de injecao (us)
uint8_t MAP = 0; //Variavel de aquisicao do valor de MAP
uint8_t RPM = 0; //Variavel de aquisicao do valor de RPM
uint8_t TAR = 0; //Variavel de aquisicao do valor de TAR
uint8_t Tinjecao = 0; //Variave de saida do Tempo de injecao
MAP = RTOS_VEM [MAP_VEM]; //Recebe do RTOS pressao em [kPa/10]
RPM = RTOS_VEM [RPM_VEM]; //Recebe do RTOS Rotacao em [RPM/100]
TAR = RTOS_VEM [TAR_VEM]; //Recebe do RTOS Temp AR em [*C/10]
//Calcula o Tempo de injecao em [us]
Tus = (2.57 * (MAP/10.13) * (288/((TAR*10)+273))) / (0.0001627296);
//Tus = (Rho*(MAP/Po)*(To/TAR)*Ncil*Vpistao)/(Vinjetor*Ninjetores*Lambda)
//Rho = 1.299[Kg/m3] - Densidade do ar atmosferico a nivel do mar
//Po = (101.3/10) [kPa] - Pressao do ar atmosferico a nivel do mar
//To = 288 [K] - Temperatura ambiente (15*C)
//Ncil = 4 - Numero de cilindros do motor
//Vpistao = 0.496 [m3]
//Vinjetor = 2.948 [ug/us] - Fluxo do injetor (microgramas por us]
//Ninjetores = 4 - Numero de injetores
//Lambda = 13.8 - Lambda para estequiometria (gasohol brasileiro)
////////////////////////////////////////////////////////////////////////
//Calcula Efeciencia Volumetrica do motor
Ev = (0.001984 * ((MAP*10000)/(8.134*(TAR*10))) * ((RPM*100)/120)) / (5.952);
//Ev = (Ereal/Eteorico)
//Ereal = Vt * (MAP/(R*TAR)) * (RPM/120)
//Eteorico = Vt * (RPMmax/2) * Evmax
//Vt = 1.984 [cm3] - Volume total do motor (converter para [m3])
//Evmax = 1 - Eficiencia volumetrica maxima
//RPMmax = 6000 [RPM] - Rotacao maxima do motor
//R = 8.134 [J/mol*C] - Constante do Gas
////////////////////////////////////////////////////////////////////////
Tinjecao = Tus * Ev; //Tempo de injecao corrigido [us/100]
*Tinj = Tinjecao; //Atualiza ponteiro de saida da funcao
if(RPM <= 6) Tinjecao = 120; //Caso Rotacao menor que 700RPM
//Determina Tinj = 10ms para partida do motor
if(Tinjecao >= 180) Tinjecao = 180; //Determina limite maximo de 18ms
if(RTOS_VEM [REGIME_VEM] == 3) Tinjecao = 0; //Se o motor esta no regime de
//desaceleracao exerce CUT-OFF
RTOS_VEM [TINJ_VEM] = Tinjecao; //Atualiza Vetor de estados
} //Final da Funcao
Essa função é executada a cada 10 ms. A função recebe os parâmetros de pressão do coletor de admissão, a rotação do motor e a temperatura do ar de admissão do vetor de estados do motor “RTOS_VEM [ ]” e efetua o cálculo do tempo de injeção em µs, conforme equação 3. Após calcular o tempo de injeção, a função calcula a eficiência volumétrica, conforme equação 4. O tempo de injeção final é corrigido pela multiplicação entre o tempo de injeção calculado e a atual eficiência volumétrica que varia entre zero e um. O tempo de injeção final é uma representação do tempo de injeção. Por exemplo, se a função retornar o valor de 146, isto significa que o tempo de injeção calculado é de 14.6 ms, o que fornece uma resolução de 100 µs. Esta conversão foi adotada para agilizar o processamento da função, considerando que utilizar variáveis do tipo “float” atrasa em até quatro vezes a velocidade de processamento da função. O resultado final é atualizado no ponteiro de saída para ser utilizado na camada de sincronismo e o vetor de estados do motor também é atualizado para que este parâmetro possa ser utilizado por outras tarefas do software.
Esse artigo apresentou uma das maneiras existentes para realizar o controle do sistema de injeção em um motor ciclo Otto, e no último artigo desta série, será apresentado o controle do sistema de admissão.
Referências
ALCÂNTARA DIAS, B. M. Unidade microcontroladora para gerenciamento eletrônico de um motor de combustão interna ciclo Otto. São Paulo. 2015. 269p. (Mestrado) Escola Politécnica, Universidade de São Paulo, São Paulo, 2015.
HENDRICKS, E. Engine Modeling for Control Applications: A Critical Survey. An Internacional Journal of Theoretical and Applied Mechanics, v. 32, n. 5, p.387-396, 1997. ISSN 1572-9648.




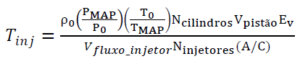










Boa noite Cynthia, excelente material. Você possui algum email de contato ? Gostaria de tirar umas duvias se possível. Att Thales (thalescarlini@gmail.com)
Olá Thales. Fico feliz que tenha gostado do material. Caso possua dúvidas, pode entrar em contato comigo em cynthiathamires@hotmail.com
Obrigado pela atenção Cynthia, estou enviando o email para você.
Boa noite Cynthia! Ótimo material porém fiquei com um dúvida na terceira equação. Nesta equação é utilizada T0 (temperatura ambiente) como 288K. Gostaria de saber o porque deste valor, visto que a temperatura ambiente varia conforme as condições do ambiente e os sistemas não apresentam meios para monitorar esta temperatura. Ao se utilizar um valor fixo não haverá um desvio do resultado obtido caso a temperatura ambiente seja diferente? Obrigado!
Boa noite Augusto.
Obrigada pelo comentário.
Você está correto. Hoje, a maioria dos veículos possuem sensores de temperatura ambiente, e esse cálculo é realizado com a informação desse sensor.
Esse projeto do artigo, foi aplicado em um veículo Polo 2004, e não possuía sensor de temperatura ambiente. Então para simplificar, colocamos um valor fixo de temperatura.
Mas você está correto, essa estratégia será melhor aplicada se for possível obter uma temperatura ambiente real.
=)
Boa tarde Cynthia!
Obrigado pelo retorno! Entendi, em função da instrumentação aplicada no sistema, utilizou-se um valor fixo na temperatura ambiente com intuito de simplificar a equação.
Muito bom os seus posts! Obrigado por compartilhar e responder! Estarei acompanhando os futuros posts. Talvez demore para responder, pois estou no último ano da graduação. Ate os próximos posts!! xD
Bom dia Cynthia
Perfeito, está correta sobre as referências! Contudo, apenas para clareza do leitor, as equações acima, que foram extraídas da dissertação do Bruno, não tem numeração. Seria bom colocar. Ademais, é importante colocar as referências nos trechos que pertencem as fontes originais. No caso da equação 2, o Bruno usou exatamente o formato das equações das minhas notas de aulas, pois em Kjellqvist não consta a descrição das variáveis da forma como eu usei e que também está no texto do Bruno. Desculpe-me pelas correções no formato do texto do artigo. É mania de professor.
Um grande abraço
Bom dia Cynthia.
É bom saber que você está ampliando a divulgação dos conhecimentos adquiridos, permitindo que mais pessoas tenham acesso. Contudo, gostaria que você corrigisse as citações, pois parte das equações acima não pertencem ao artigo da Hendricks, mas sim à minhas notas de aula, das quais você participou durante a sua graduação.
Grato.
Prof. Edson
Boa noite professor Edson. Fico feliz em saber que o senhor acompanha meus artigos. O senhor foi fundamental para minha formação e suas aulas foram de extrema importância. Foi onde tudo começou e de fato essa série de artigos nasceu com o conteúdo ministrado pelo senhor nas suas aulas. Sem dúvida alguma, suas aulas foram parte fundamental de tudo que publicamos sobre o gerenciamento do motor, bem como toda a formação que tivemos na FATEC Santo André. Essa série de artigos sobre o gerenciamento do motor, foi baseada na dissertação do Bruno, que referencia todas as equações seguindo a ética… Leia mais »
Muito bom Cynthia, gosto da forma clara e simplificada que tu apresenta o tema. Parabéns!