Neste artigo vamos analisar o comportamento dos circuitos RLC em paralelo, excitados pelas condições iniciais dos componentes de armazenamento, ou seja, não contém fontes independentes, apesar de poder conter fontes dependentes. E depois, avaliaremos o comportamento dos circuitos submetidos a uma fonte independente.
Circuitos RLC em paralelo sem fonte
Vamos iniciar considerando o circuito RLC em paralelo mostrado na Figura 1, observamos um circuito que é excitado pela energia inicialmente armazenada no capacitor e indutor. A tensão inicial é representada por V0 no capacitor e a corrente inicial é I0 no indutor.
Assim, em t = 0:
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
Como os três componentes passivos estão em paralelo, eles possuem a mesma tensão v neles. Considerando positiva a corrente que sai do nó, ao aplicar a LKC ao nó superior, temos:
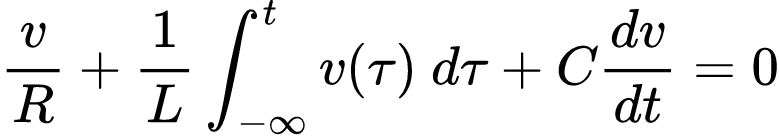
Para remover a integral, diferenciamos em relação a t, dividimos por C e reorganizamos os termos para deixar no formato de equação diferencial de segunda ordem.
Para obter a equação característica basta substituir a primeira derivada por s e a segunda por s2. Assim, temos:
Logo, as raízes da equação característica são:
Em termos de α e ω0, as raízes são:
Em que:
A nomenclatura dos termos permanece a mesma apresentada no artigo de Circuitos RLC em Série, onde ω0 é conhecido como frequência natural não amortecida ou frequência ressonante e α é o fator de amortecimento ou frequência de neper.
De maneira análoga aos circuitos em série, dependendo dos valores de α e ω0 é possível ter três tipos de soluções:
- Caso de amortecimento supercrítico (α > ω0)
Para α ser maior ω0 é preciso que:
Quando isso ocorre, as raízes s1 e s2 são negativas e reais. A resposta, então, é:
- Caso de amortecimento crítico (α = ω0)
Para α ser igual a ω0:
Isso implica em duas raízes (s1 e s2) reais e iguais. Nesse caso, a resposta é:
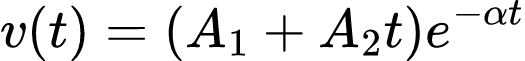
- Caso de subamortecimento (α < ω0)
Para α menor que ω0:
Isso implica em duas raízes (s1 e s2) complexo conjugadas. Logo:
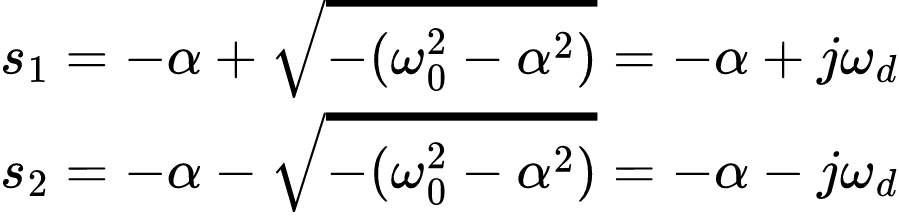
Em que:
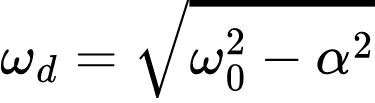
ωd é chamado de frequência de amortecimento. Lembrando que ω0 é chamada frequência natural não amortecida, já ωd é chamada frequência natural amortecida.
A resposta natural, nesse caso, é:
Em todos os casos, as constantes A1 e A2 são determinadas a partir das condições iniciais v(0) e dv(0)/dt. v(0) já conhecido e é igual ao V0 (tensão no capacitor), já dv(0)/dt é obtido através de:
As formas de onda da tensão do circuito depende se ele é do tipo amortecimento supercrítico, subamortecimento ou amortecimento crítico e possuem formato semelhante às mostradas no artigo Circuito RLC em Série.
Uma vez determinada a tensão v(t) no capacitor para o circuito RLC em paralelo, é possível obter outros valores para o circuito, como as correntes em cada elemento.
Exemplo RLC em série sem fonte
Considerando a Figura 2, vamos determinar v(t) para t>0 supondo que v(0) = 5 V, i(0) = 0 A.
Primeiro, vamos determinar α e ω0:
Como α = ω0, a resposta será do tipo amortecimento crítico, com duas raízes reais e iguais. Estas raízes são:
Logo, v(t) terá o seguinte formato:
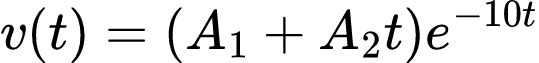
Para determinar A1 e A2, precisamos aplicar as condições iniciais:
Derivando a equação de v(t):
Aplicando em t=0, temos que A2 é:
Portanto, a equação da tensão é:
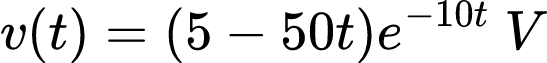
Resposta a um degrau de um circuito RLC em série
A resposta a um degrau é obtida ao aplicar, de forma repentina, uma fonte CC. Considerando o circuito RLC em paralelo, mostrado na Figura 2, iremos determinar i devido a fonte de corrente aplicada.
Aplicando a LKC ao nó superior para t > 0:
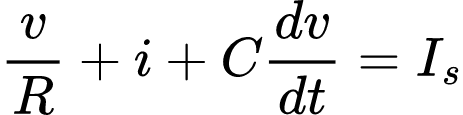
Como v é dado por:
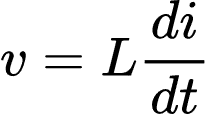
Então, iremos substituir v e ter:
A equação encontrada tem a mesma forma da equação para o circuito sem fonte de tensão. Ao observar com atenção, vemos que os coeficientes são os mesmos, mas, a variável é diferente.
Portanto, a equação característica para o circuito RLC em paralelo não é afetada pela presença da fonte CC.
A solução completa para a equação possui duas componentes: uma resposta transiente it(t) e resposta de estado estável iss(t).
A resposta transiente é a mesma obtida para o circuito sem fonte, um detalhe é que a resposta de estado estável é o valor final de i, no circuito observado o valor final da corrente que passa no indutor é o mesma que a corrente da fonte Iss.
Logo:
| Resposta Completa | Tipo |
 | Amortecimento supercrítico |
 | Amortecimento crítico |
 | Subamortecimento |
Lembrando que os valores das constantes A1 e A2 são obtidos das condições iniciais, nesse caso de i(0) e di(0)/dt.
Outro ponto importante é que v e i são, respectivamente, a tensão no capacitor e a corrente que atravessa o indutor. Então, a equação que obtemos se aplica somente para determinar i.
Mas, uma vez que a tensão no capacitor (iL = i) for conhecida, é possível determinar a tensão v = L di/dt, que será a mesma tensão através dos 3 elementos passivos. Portanto, a corrente no resistor é iR = v/R, já a corrente no capacitor é ic = C dv/dt.
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
