Análogo aos circuitos formados por resistores e capacitores (RC), os circuitos RL também são de primeira ordem, ou seja, são descritos por equações diferenciais de primeira ordem.
Neste artigo vamos analisar o comportamento e determinar as equações de saída de um circuito RL sem fonte e com uma entrada degrau.
Circuitos RL sem fonte
Um circuito RL sem fonte ocorre da mesma forma que um circuito RC sem fonte. A diferença é que o objeto da análise do RL é a corrente i(t) por meio do indutor. A escolha da resposta foi pensada no fato da corrente do indutor não poder mudar instantaneamente.
Para entender o funcionamento desse circuito, vamos considerar o circuito mostrado na Figura 1.
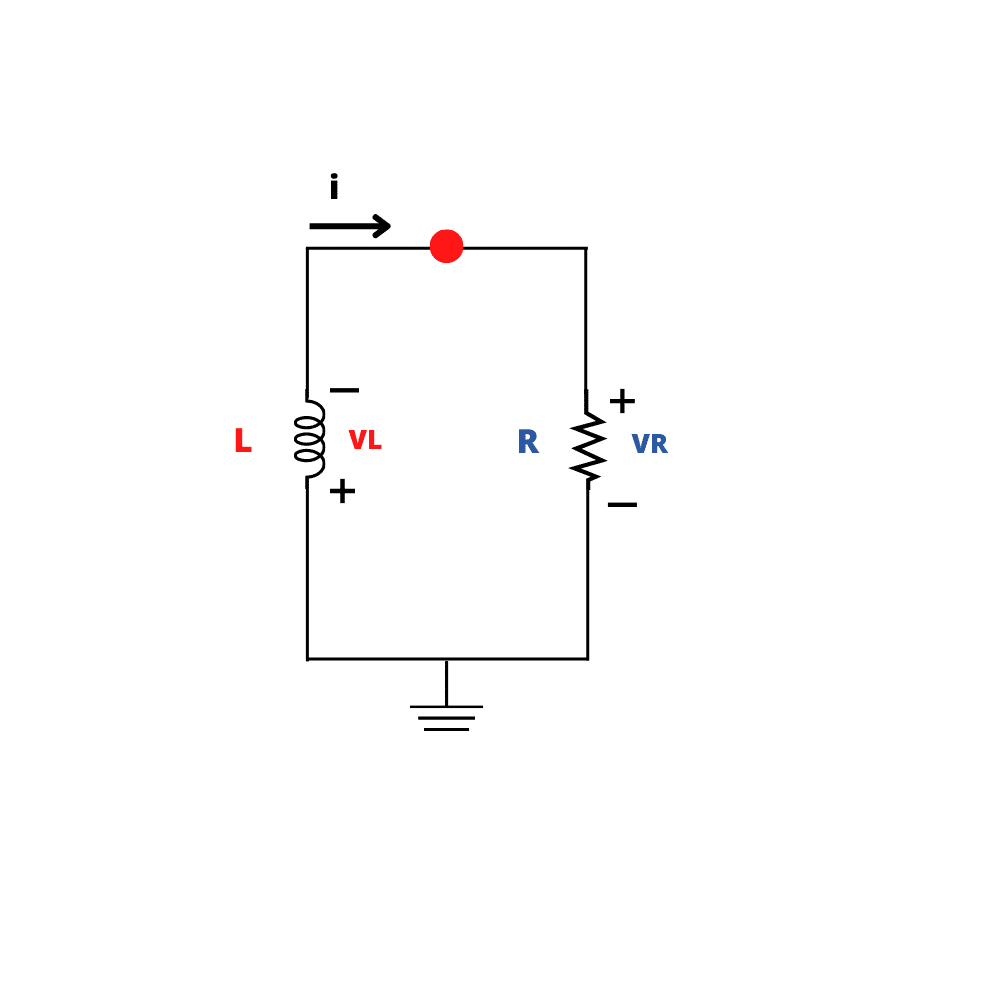
Assim, assumimos que t = 0 o indutor tenha uma corrente inicial Io, ou seja:

E a energia armazenado no instante 0 é dada por:

Ao aplicar LKT no laço, temos que a tensão é:

Por definição, temos:

Logo:

Rearranjando os termos e integrando para determinar i(t), temos:

O resultado final encontrado é que a resposta em corrente do circuito RC é uma queda exponencial da corrente inicial. Pela equação também é possível inferir que a constante de tempo T (em segundos) é dada por:

Logo, a resposta pode ser reescrita como:
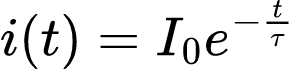
Graficamente fica mais fácil visualizar esse comportamento. Observe na Figura 2, que quanto menor a constante de tempo T de um circuito, mais rapidamente a resposta decai. Ao aumentar a constante de tempo, a taxa de decaimento da resposta fica mais lenta. Além disso, após 5T ela atinge seu regime estacionário.

Fonte: ALEXANDER (2013).
Com a equação da corrente, podemos determinar a tensão no resistor:

Já a potência dissipada no resistor é dada por:
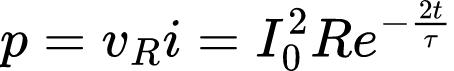
Enquanto que a energia absorvida pelo resistor é:
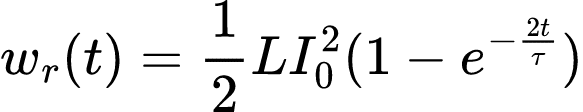
É possível notar que t tende a infinito wr tende a 1/2LI02. Isso é o igual a wL(0) (energia armazenada inicialmente no indutor). Isso significa dizer que toda a energia que estava armazenada inicialmente no indutor é dissipada no resistor.
Em resumo, para se trabalhar com um circuito RL sem fonte é necessário determinar:
- A corrente inicial i(0) = Io no indutor
- A constante de tempo τ do circuito.
Exemplo RL sem fonte
Para entender como trabalhar com circuitos RL, faremos um exemplo. Considerando o circuito da Figura 3, com i(0) = 10 A, para calcular i(t) e ix(t) no circuito.
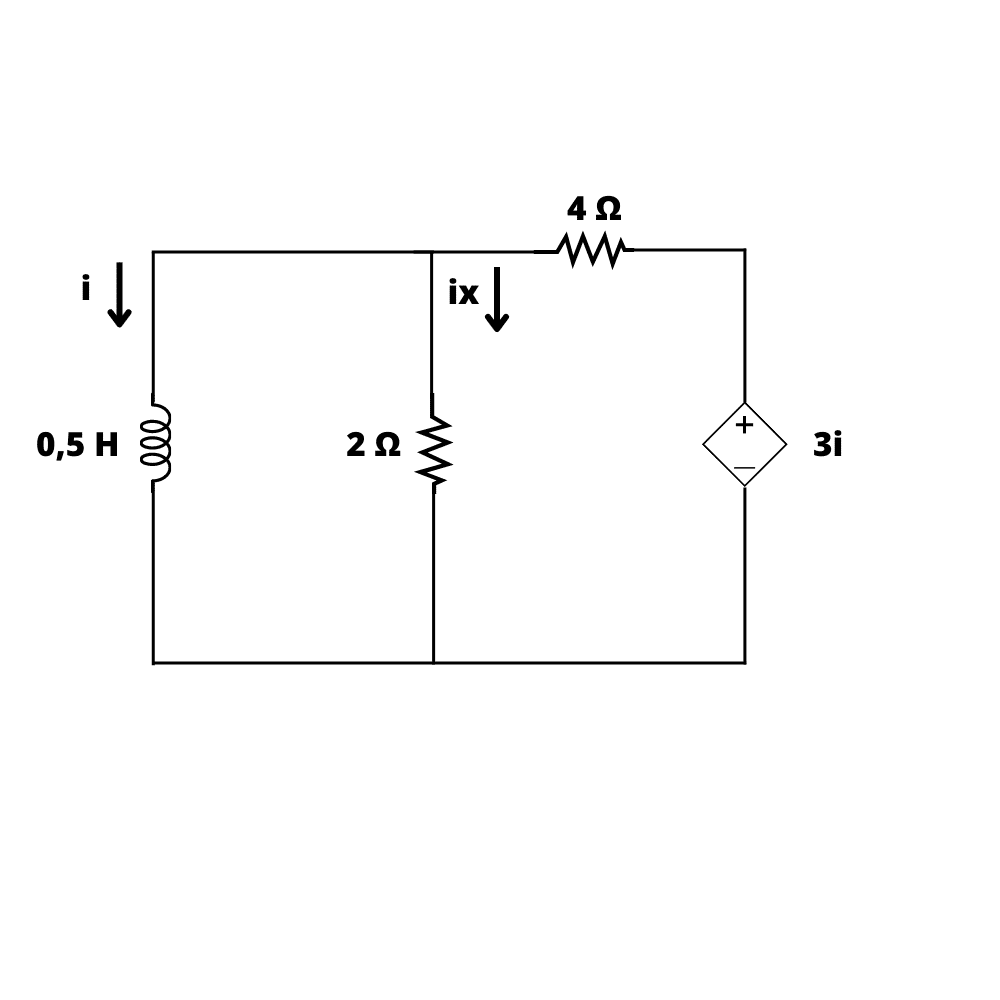
Assumindo duas malhas, vamos aplicar LKT na malha 1 (M1) e depois na malha 2 (M2).

O resultado encontrado:
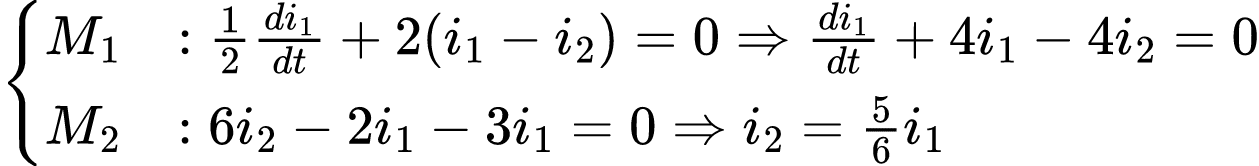
Substituindo a equação de M1 em M2:

Como i1 = i, podemos realizar a substituição e integrar:

Reescrevendo em termo de exponencial e isolando i(t), encontramos:

Assim, a tensão no indutor será:
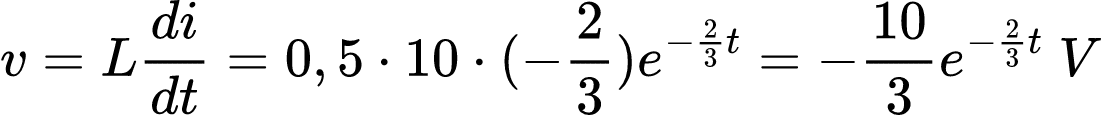
Como o indutor e o resistor de 2 Ω estão em paralelo, temos que ix(t) será:

Resposta a um degrau de um circuito RC
Agora vamos entender o comportamento do circuito quando submetido a fonte de tensão ou de corrente modelada como uma função degrau. A resposta para esse tipo de entrada é conhecida como resposta a um degrau.
Para entender esse comportamento, vamos considerar o circuito RL da Figura 5.

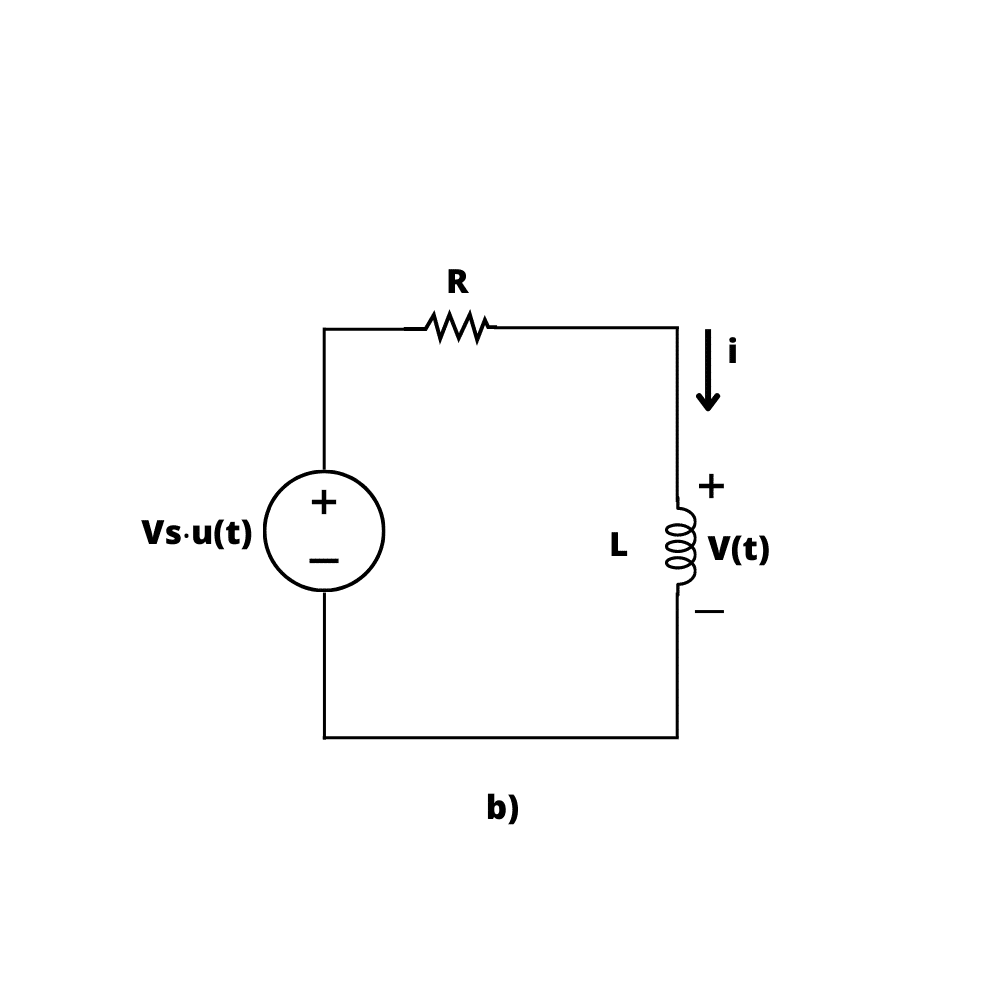
A resposta pode ser a soma da resposta transiente e a resposta em regime estacionário, já mencionadas no artigo sobre circuito RC, logo:
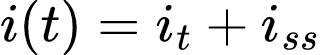
onde:

A resposta transiente (it) e sempre é uma exponencial em queda. Lembrando que A é a constante a ser determinada. Já a resposta em regime estacionário (iss) é o valor da corrente depois que um tempo se passou desde que a chave foi fechada.
Como no circuito RC, a resposta transiente basicamente zera após cinco constantes de tempo. Quando isso ocorre, o indutor torna-se um curto-circuito e a tensão nele é zero. Por essa razão iss é escrito com toda a tensão de entrada Vs sobre R.
Para determinar a constante A do valor inicial da corrente. Consideramos que I0 é a corrente inicial pelo indutor, (proveniente de uma fonte que não seja Vs).

Assim, em t = 0 temos:

Substituindo A temos a resposta completa ao degrau:
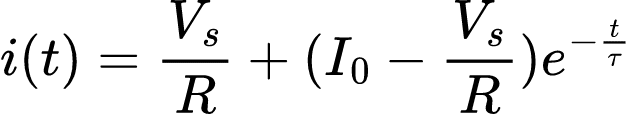
Em resumo, para se trabalhar com um circuito RL com resposta ao degrau é necessário determinar:
- A corrente inicial i(0) no indutor em t = 0
- A corrente final i(∞) no indutor
- A constante de tempo τ
É válido ressaltar que obtemos o item 1 do resumo para t < 0 e os itens 2 e 3 do circuito para t > 0.
Referência
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
















