Para facilitar a análise de circuitos, frequentemente há a necessidade de associar resistores. Esse processo é realizado com resistores ôhmicos, cuja resistência é constante, os quais podem ser associados em série ou paralelo.
O fator determinante de qual tipo de associação deverá ser feita é a corrente elétrica e a diferença de potencial. Neste artigo, vamos entender como essas associações são feitas.
Associação de Resistores em Série
A associação de resistores em série pode ser feita quando há dois ou mais resistores percorridos pela mesma corrente i. Assim, considere o circuito com um único laço da Figura 1.
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
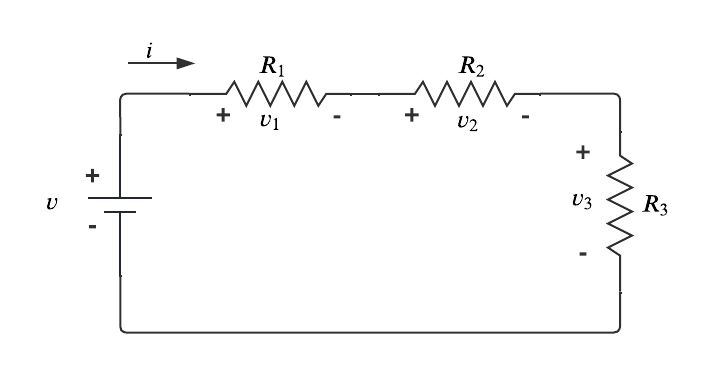
Observe que os três resistores estão em série, pois a mesma corrente i flui por eles. Ao aplicar a Lei de Ohm a cada um dos resistores, obtemos:
Note que apesar de compartilhar da mesma corrente, a diferença de potencial em cada resistor irá variar de acordo com a sua resistência.
Ao aplicar a Lei das Malhas no laço percorrendo no sentido horário e assumindo a tensão é positiva ao sair do terminal negativo para o positivo, temos:
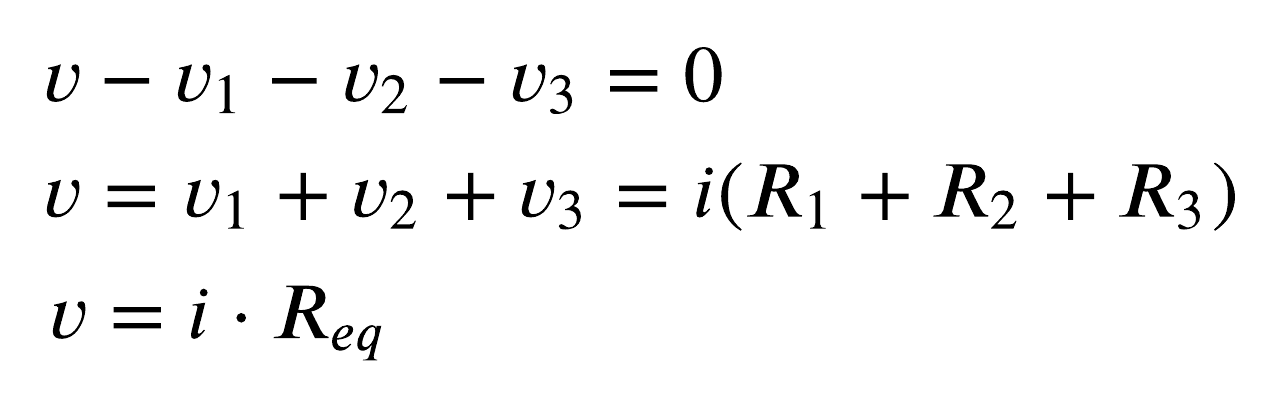
Isso nos mostra que quando os resistores compartilham da mesma corrente (ou seja, estão em série), basta substituí-los por um único resistor Req.
A resistência de Req será a soma das resistências individuais dos resistores ligados em série.
Logo, para N resistores em série, temos:
Associação de Resistores em Paralelo
Já a associação de resistores em paralelo pode ser feita quando dois resistores possuem dois pontos em comum. Outro importante detalhe é que os elementos em paralelo possuem a mesma diferença de potencial. Assim, considere o circuito mostrado na Figura 2.
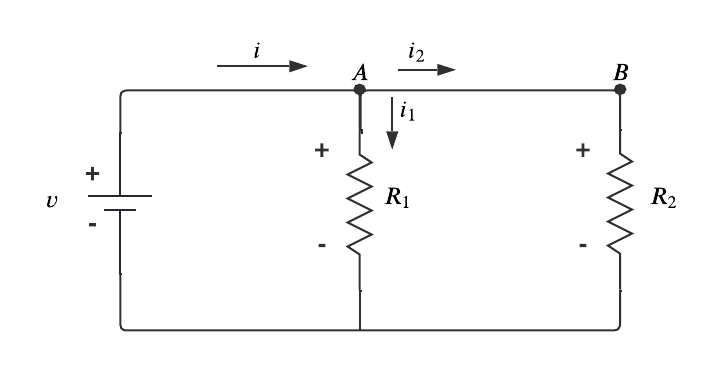
Ao aplicar a Lei de Ohm a cada um dos resistores, obtemos:
A tensão do gerador (v) é igual à tensão sobre o resistor 1 e 2, pois os três estão em paralelo. Note que ao compartilhar da mesma diferença de potencial, a corrente em cada resistor irá variar, para identificar a corrente aplicamos a Lei dos Nós.
Ao aplicar a Lei dos Nós no nó A, assumindo que a corrente que entra no nó é positiva, temos:
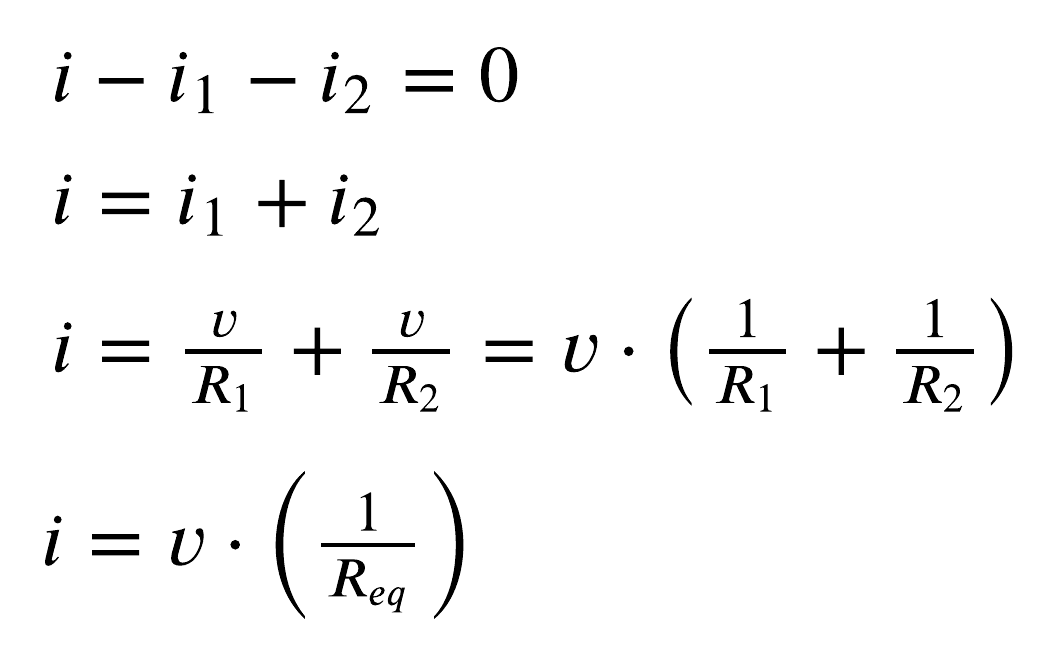
Assim, quando os resistores compartilham da mesma diferença de potencial (ou seja, estão em paralelo), basta substituí-los por um único resistor Req. Esse resistor equivalente, para um número qualquer de resistores, é dado por:
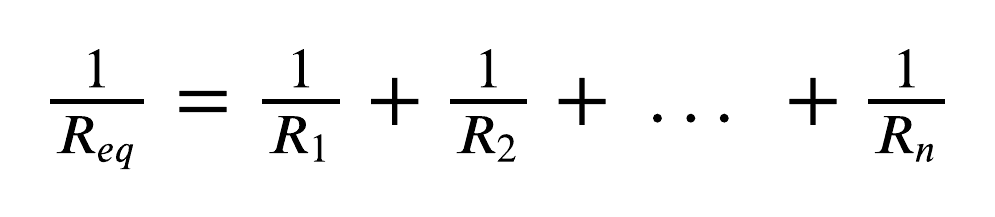
Há dois casos especiais na associação em paralelo. O primeiro é quando há, somente, dois resistores em paralelo:
A resistência Req de dois resistores em paralelo é o produto de suas resistências dividido pela sua soma.
Então matematicamente, temos a seguinte simplificação da fórmula:
O segundo caso é quando todos os resistores em paralelo têm valores iguais, logo:
Como temos a soma de frações com o mesmo denominador, o denominador é conservado e os numeradores são somados. Os numeradores têm valor 1, então a soma será igual ao número de resistores em paralelo (n). Por essa razão, temos essa segunda simplificação da fórmula da associação de resistores.
Associação Mista
A associação mista ocorre quando há a combinação de associações em paralelo e em série no mesmo circuito. É muito comum encontrar associações mistas em circuitos elétricos, uma dica para não errar os cálculos é resolver cada associação separada e redesenhar o circuito.
Na Figura 3 é possível notar que R1 e R2 estão em paralelo, por possuírem dois pontos em comum, então, o primeiro passo é resolver essa associação.
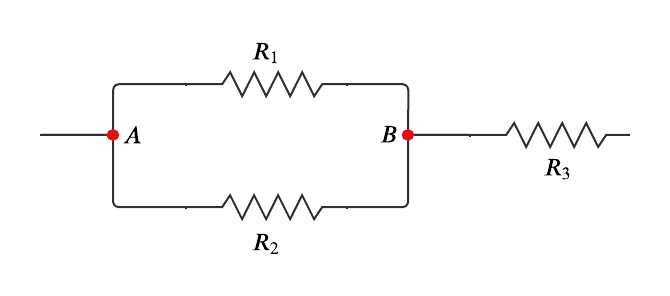
Resolvida a associação em paralelo de R1 e R2 encontramos R1,2. Ao redesenhar o circuito observamos que R1,2 está em série com R3. Então, resta resolver a associação em série de R1,2 e R3 para encontrar resistor equivalente (Req) do circuito.
Resumo
Para fixar na memória a diferença entre a associação de resistores em série e em paralelo, utilize a Tabela 1.
| Associação em Série | Associação em Paralelo | |
| Diferença de Potencial | vn = i‧Rn | Igual para todos os resistores |
| Corrente | Igual para todos os resistores | in = v/Rn |
| Resistência Equivalente | Req = R1 + R2 + … + Rn | 1/Req = 1/R1 + 1/R2 + …. + 1/Rn |
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.
