Os indutores, assim como os resistores e capacitores, podem ser ligados em série ou em paralelo. A estratégia permite o aumento da indutância conectando os indutores em série e uma diminuição é obtida conectando-os em paralelo, como ocorre com os resistores.
Nesse artigo vamos entender como substituir as associações em série ou em paralelo dos indutores por um único indutor equivalente Leq.
Associação de Indutores em Série
A associação de indutores em série pode ser feita quando há dois ou mais indutores, como pode ser visto no circuito com um único laço da Figura 1.
Os Melhores Treinamentos sobre Sistemas embarcados e IoT
Cursos com professores qualificados para acelerar sua carreira e projetos
Os indutores têm a mesma corrente passando por eles. Assim, aplicando a LKT, encontramos que:
Da definição de indutância, temos que a tensão é dada por:
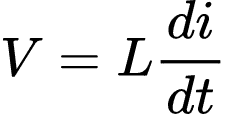
Logo:
Isolando di/dt obtemos:
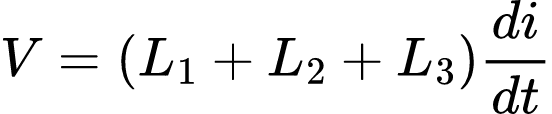
Ou seja o Leq, será:
Observe que o resultado encontrado é igual à equação para o cálculo da resistência total de um circuito resistivo em série.
Para N indutores em série, temos:
Associação de Indutores em Paralelo
Já no caso de indutores em paralelo, o esquema é o mostrado no circuito da Figura 2.
Os elementos em paralelo compartilham da mesma diferença de potencial.
Usando a LKC, a corrente total é a soma das correntes dos indutores.
Da definição temos que a corrente é dada por:
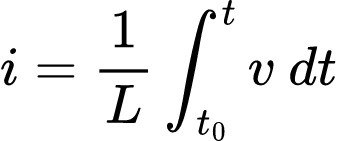
Logo:
Como a tensão é a mesma, temos:
Ou seja o Leq, será:
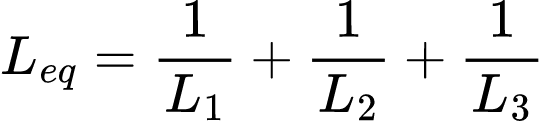
Note que é igual à equação usada para calcular a resistência total de um circuito resistivo em paralelo.
Para N indutores em paralelo, temos:
Comparativo: Associação de Indutores Vs Associação de Resistores e Associação de Capacitores
Nesta tabela há um resumo das associações de resistores, capacitores e indutores.
| Associação em Série | Associação em Paralelo | ||
| Diferença de Potencial | Vn = i‧Rn | Igual para todos os resistores | |
| Resistores | Corrente | Igual para todos os resistores | in = v/Rn |
| Resistência Equivalente | Req = R1 + R2 + … + Rn | 1/Req = 1/R1 + 1/R2 + …. + 1/Rn | |
| Diferença de Potencial | Vn = Q/CN | Igual para todos os capacitores | |
| Capacitores | Carga | Igual para todos os capacitores | Qn = Cn‧V |
| CapacitânciaEquivalente | 1/CT = 1/C1 + 1/C2 + …. + 1/Cn | CT = C1 + C2 + … + Cn | |
| Diferença de Potencial | V=L‧di/dt | Igual para todos os indutores | |
| Indutores | Corrente | Igual para todos os indutores | in = 1/Ln ∫v dt |
| Indutância Equivalente | Leq = L1 + L2 + … + Ln | 1/Leq = 1/L1 + 1/L2 + …. + 1/Ln |
Referências
ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.
BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.
Creio que existe um erro (associação paralela), Leq não é a soma dos inversos, e sim o inverso da soma dos inversos.