Teorema de Thévenin

A diversidade do uso de circuitos elétricos em diferentes áreas possibilitou a evolução de circuitos simples para complexos e as leis de Kirchhoff, até então muito utilizadas, tornaram-se desvantajosas por gerar cálculos grandes e cansativos. Assim, ao longo dos anos, foram desenvolvidos teoremas que mudam a configuração original do circuito na intenção de simplificar a análise, como o teorema de Thévenin cujo destaque será dado neste artigo.

O teorema de Thévenin, assim como o teorema de Norton, é aplicável apenas em circuitos lineares, então será primeiramente abordado o conceito de linearidade em circuitos, para depois esclarecer como o teorema funciona.

Circuitos Lineares

A linearidade de um componente descreve que há uma relação diretamente proporcional entre a entrada e saída. Essa propriedade é uma combinação das propriedades de homogeneidade e da aditividade. Apesar da linearidade funcionar para vários elementos de circuitos, destacamos sua aplicabilidade aos resistores.

Começando com a homogeneidade, essa propriedade dita que: se a entrada (ou excitação) for multiplicada por uma constante qualquer, então a saída (ou resposta) também deve ser multiplicada pela mesma constante. Nos resistores essa relação entrada-saída é visualizada através da lei de Ohm.

Os Melhores Treinamentos sobre Sistemas embarcados e IoT

Cursos com professores qualificados para acelerar sua carreira e projetos

MATRÍCULE-SE AGORA

Logo, se a corrente for aumentada por uma constante k, então a tensão aumenta igualmente um valor k:

Já a aditividade dita que a saída para uma soma de entradas deve ser a soma das saídas a cada entrada aplicada separadamente. Usando a relação tensão-corrente de um resistor, temos:

Então aplicar (i₁+ i₂) resulta em:

    Portanto, conclui-se que um resistor é um componente linear por satisfazer tanto as propriedades de homogeneidade quanto de aditividade. Nesse sentido, normalmente, um circuito é linear quando formado por elementos lineares e fontes lineares dependentes e independentes.

Teorema de Thévenin

    Nesse sentido, de modo geral, dado um circuito linear o teorema de Thévenin auxilia quando:

• O circuito possui complexidade, dificultando a análise pelas leis dos nós ou das malhas;
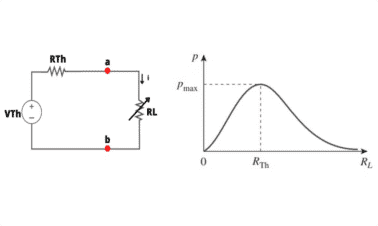
• Um determinado elemento do circuito é variável (esse componente, geralmente, é chamado carga) enquanto outros elementos são fixos. Para avaliar o comportamento do sistema cada vez que o elemento variável é alterado, substituir a parte fixa por um circuito equivalente é mais vantajoso.

    Assim, o teorema afirma que:

Um circuito linear de dois terminais pode ser substituído por um circuito equivalente formado por uma fonte de tensão V_Th (tensão de Thévenin) em série com um resistor R_Th (resistência de Thévenin).

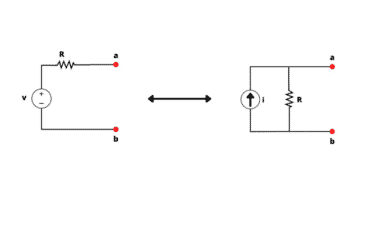
    Para entender como qualquer circuito linear pode ser simplificado para uma tensão de Thévenin em série com um resistor de Thévenin, suponha que os dois circuitos abaixo são equivalentes.

 Para assumir isso, primeiramente é preciso saber que dois circuitos são considerados equivalentes se possuem a mesma relação tensão-corrente em seus terminais. Então, tornando os terminais a-b, da Figura 1b, em um circuito aberto (ou seja, eliminando a carga), nenhuma corrente fluirá no circuito.

Logo, a tensão V_oc (tensão de circuito aberto) nos terminais a-b da Figura 2a tem valor igual à fonte de tensão V_Th. Devido à equivalência dos circuitos, a tensão de circuito aberto da Figura 2b também é V_Th. Portanto, V_Th nada mais é do que a tensão de circuito aberto nos terminais, como mostra a Figura 2.

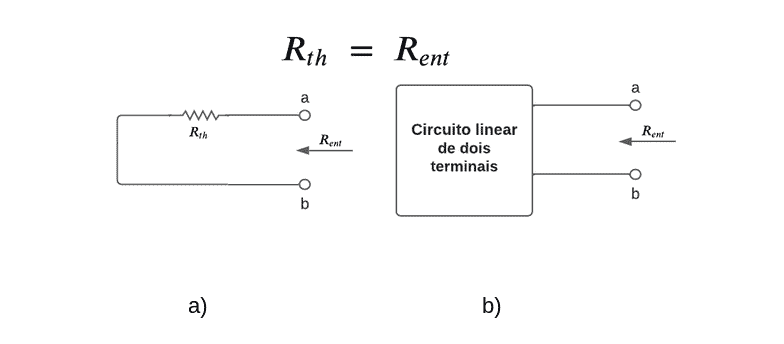
Ainda com os terminais em circuito aberto (carga removida), todas as fontes independentes são desligadas para definir o R_Th. Com isso, pode-se observar que a resistência de entrada (ou equivalente) do circuito inativo, mostrado na Figura 3a, é igual a R_Th, o mesmo vale para o circuito equivalente na Figura 3b. Portanto, R_Th simplesmente é a resistência de entrada nos terminais quando as fontes independentes estão desligadas.

Procedimento do teorema de Thévenin 

    Entendido que o V_Th  é a tensão de circuito aberto nos terminais observados e que o R_Th é a resistência de entrada vista entre os terminais observados, há uma série de passos que o levarão ao valor adequado de cada parâmetro do circuito equivalente.

O procedimento é o seguinte:

1. Remova a parte do circuito em que se objetiva obter o equivalente de Thévenin;
2. Calcule R_Th
   1. Desligando as fontes independentes (fontes de tensão são substituídas por curto circuito e fontes de corrente por circuitos abertos);
   2. Determine a resistência equivalente entre os dois terminais escolhidos.
3. Calcule V_Th
   1. Volte a considerar os valores das fontes de tensão e de corrente;
   2. Determine a tensão entre os dois terminais escolhidos, lembrando que a diferença de potencial deve ser calculada com o circuito aberto entre os terminais.

Conclusão

Neste artigo foi apresentado para que serve o teorema de Thévenin, em que situação e como é possível usá-lo. Assim, foi visto que o teorema surgiu como uma ferramenta para simplificar circuitos complexos e que só é aplicável em circuitos lineares. Além disso, foi definido que a tensão de Thévenin (V_Th) é a tensão de circuito aberto nos terminais e a resistência de Thévenin (R_Th) é a resistência de entrada – ou equivalente – nos terminais quando as fontes independentes forem desativadas. 

Por último, foi mostrado o procedimento de obtenção dos parâmetros V_Th e R_Th do circuito equivalente. 

Referências

ALEXANDER, Charles K.. Fundamentos de circuitos elétricos. Porto Alegre: Amgh, 2013.

BOYLESTAD, Robert L.. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2012.