Introdução
No artigo Conversor A/D – Trazendo o mundo real para dentro do processador foram mostrados alguns efeitos decorrentes da quantização de um sinal analógico num número finito de valores inteiros, definido pelo número de bits de resolução de um conversor Analógico / Digital. Neste artigo serão apresentados alguns recursos interessantes que o processamento digital de sinais pode oferecer. A sobre-amostragem (oversampling), aumento artificial da taxa de amostragem (upsampling) seguida de uma filtragem de reconstrução, ou interpolação, e a decimação (downsampling), que é a redução artificial da taxa de amostragem. São técnicas de processamento digital de sinais simples, porém muito poderosas.
Oversampling
Dá-se o nome de Oversampling à ação de realizar uma amostragem do sinal muito acima da frequência mínima de amostragem, determinada pelo critério de Nyquist-Shannon, ou seja, no mínimo 2 vezes a maior frequência do sinal a ser digitalizado. É boa prática amostrar o sinal com taxas de pelo menos 8 a 10 vezes a maior frequência do sinal. Para se fazer um oversampling, pode-se utilizar taxas maiores que 32 vezes a frequência mínima.
Por que fazer um oversampling?
Existem dois motivos principais para se utilizar desse recurso. O primeiro motivo é a simplificação do filtro analógico de anti-aliasing na entrada do conversor A/D, necessário para evitar o aparecimento de frequências fictícias na faixa útil do sinal decorrentes dos efeitos da amostragem. No caso de oversampling, pode ser utilizado um filtro passivo simples do tipo R-C, que muitas vezes já está incorporado aos conversores A/D, dispensando o uso de filtros analógicos ativos. Se necessário, pode-se aplicar ainda um filtro digital para reduzir ainda mais os sinais indesejados. O segundo motivo é o aumento de resolução em número de bits. A relação entre o aumento de resolução em bits e a taxa de amostragem mínima é a seguinte:
Isso funciona, desde que o sinal seja periódico e o conversor A/D possua uma linearidade que não comprometa essa ação. Ao longo do texto serão apresentados scripts desenvolvidos para o programa Octave, que geraram os dados e as figuras apresentadas a seguir. O leitor pode copiar esses scripts e simular essas e outras situações que desejar. Será necessário também instalar o pacote adicional do Octave com funções de processamento digital de sinais, o pacote Signal.
O script a seguir gera uma senoide ideal que servirá de base para o oversampling e a posterior quantização.
% Gera e plota uma senoide ideal amostrada com oversampling
Num_Bits_Ovr = 0; % Define número de bits adicionais desejados
Num_Amostras = 16 * 4^Num_Bits_Ovr; % Define o número de amostras por ciclo
Num_Ciclos = 4; % Define o número de ciclos
Delta_t = 1/Num_Amostras; % Define o delta t entre as amostras
tempo = 0:Delta_t:Num_Ciclos - Delta_t; % Define os tempos para gerar a senoide
seno1 = 0.5 * (1 + sin(2 * pi * tempo)); % gera a senoide
close all; % Fecha todas as figuras
figure(1); % Abre a figura 1
plot(seno1); % Plota o seno na figura 1
hold; % Retém a figura
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
title('Senoide ideal amostrada');
plot(seno1, 'x'); % Marca os pontos amostrados
seno1 = seno1 - 0.5; % Suprime a componente CC
figure(2); % Abre a figura 2
fftseno1 = abs(fft(seno1)); % prepara a FFT
plot(20 * log10(fftseno1/max(fftseno1))); % Plota a FFT normalizada em dB
grid; % Gera a grade
xlabel('Frequencias');
ylabel('Amplitude normalizada em dB');
title('FFT da senoide ideal amostrada');
%
O script a seguir gera a quantização e o espectro (FFT) do sinal gerado pelo script anterior, assim se pode observar os efeitos do oversampling.
% Gera a quantização da senoide ideal
Numero_de_Bits = 8; % Especifica o numero de bits
%Gera ruido de quantização aleatório
ruido = (rand(length(seno1),1) -0.5) / 2^Numero_de_Bits;
senoq = seno1 + ruido'; % Gera a senoide com ruido de quantização
Cte = (2^Numero_de_Bits) - 1; % Calcula a potência de 2
seno1_quantizado = round(senoq * Cte); % gera o seno quantizado sem a componente CC
figure(3); % Abre a figura 3
fftseno1_quant = abs(fft(seno1_quantizado)); % Prepara a FFT
plot(20 * log10((fftseno1_quant/max(fftseno1_quant))+ 10^-16)); % Plota a FFT
grid; % Gera a grade
xlabel('Frequencias');
ylabel('Amplitude normalizada em dB');
title('FFT da senoide quantizada amostrada');
%
Na Figura 1 a seguir pode-se observar o espectro da senoide amostrada com taxa de 16 amostras por ciclo e quantizada para 8 bits.
Se aplicarmos uma sobre-amostragem de 256 vezes, rodando o script alterando, o valor de Num_Bits_Ovr para 4, visando aumentar a resolução para 12 bits, obtemos o espectro mostrado na Figura 2.
Observando a Figura 2, pode-se notar que o número de amostras é muito grande (64 vezes maior). E vale lembrar que resolução não é o mesmo que precisão. Muitos conversores A/D especificam um parâmetro chamado de EOB (Efective number of bits – número efetivo de bits), que sempre é menor que a resolução do conversor A/D e determina a efetiva precisão do componente. Para fins de comparação observe a Figura 3, onde está retratada a FFT de uma senoide, amostrada 16 vezes por ciclo, quantizada para 12 bits de resolução. Repare que o nível do ruído de quantização se encontra num nível semelhante ao do espectro obtido após o oversampling.
Upsampling
Upsampling é um técnica de processamento digital de sinais para aumentar artificialmente a taxa de amostragem em N vezes, inserindo um número N-1 de zeros entre as amostras originais do sinal, e passando o conjunto obtido por um filtro de reconstrução, que nada mais é que um filtro do tipo passa-baixas. Para mostrar essa técnica utilizaremos o programa anterior ligeiramente modificado. O script a seguir simula o upsampling da senoide ideal e realiza a filtragem de reconstrução.
% Gera e plota uma senoide ideal amostrada com upsampling
Num_Amostras = 16; % Define o número de amostras por ciclo
Num_Ciclos = 4; % Define o número de ciclos
Delta_t = 1/Num_Amostras; % Define o delta t entre as amostras
tempo = 0:Delta_t:Num_Ciclos - Delta_t; % Define os tempos para gerar a senoide
seno1 = 0.5 * (1 + sin(2 * pi * tempo)); % gera a senoide
close all; % Fecha todas as figuras
figure(1); % Abre a figura 1
plot(seno1); % Plota o seno na figura 1
hold; % Retém a figura
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
title('Senoide ideal amostrada');
plot(seno1, 'x'); % Marca os pontos amostrados
seno1 = seno1 - 0.5; % Suprime a componente CC
figure(2); % Abre a figura 2
fator_up = 8; % Define fator de upsampling
up = upsample(seno1,fator_up);
plot(up);
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
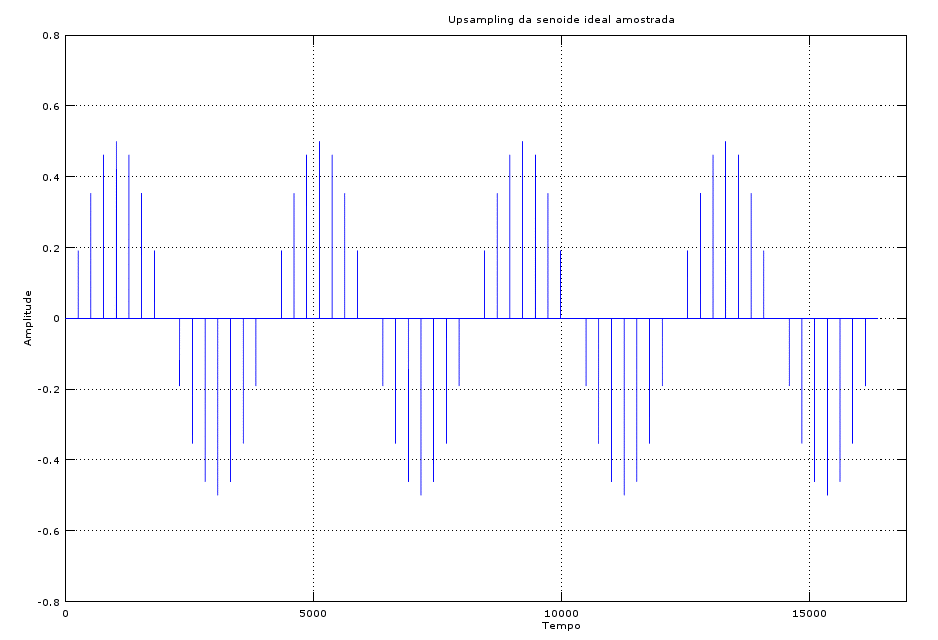
title('Upsampling da senoide ideal amostrada');
%
Na Figura 4 pode-se observar como fica o sinal original intercalado com zeros entre as amostras, nesse caso com 255 zeros (fator_up = 256).
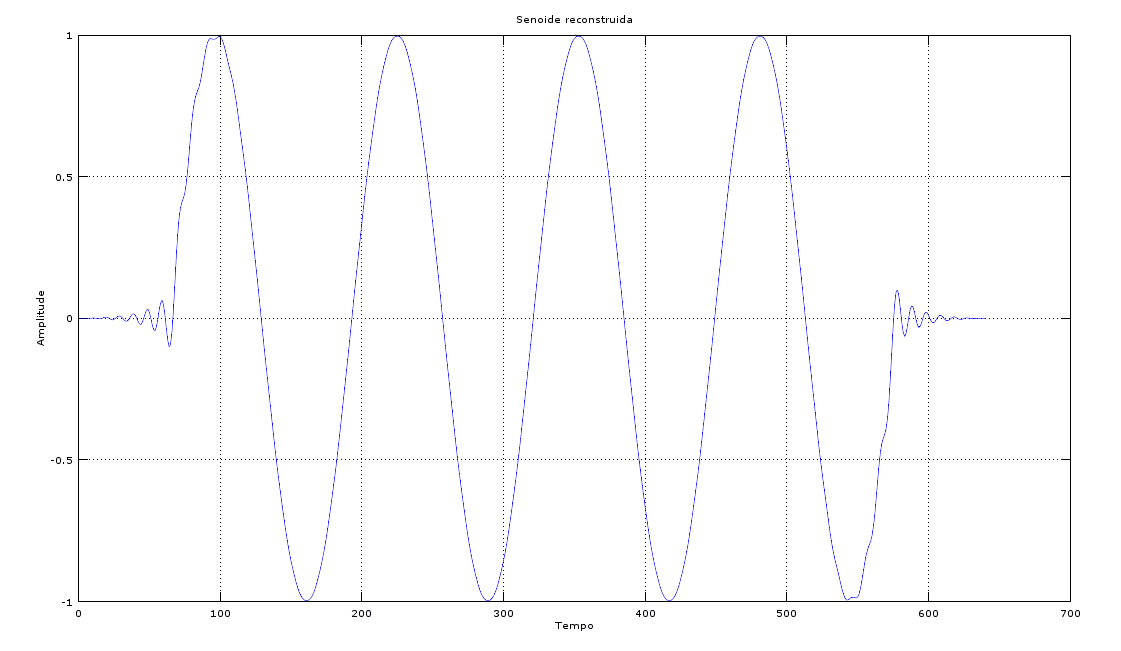
Evidentemente essa técnica impõe limites de aplicação. É intuitivo o fato que quanto maior a interpolação, mais a informação referente ao sinal original é distorcida ou perdida. Na Figura 5 pode-se observar a forma de onda resultante após a reconstrução da senoide original interpolada para aumentar a taxa de amostragem em 8 vezes (fator_up = 8). O filtro de reconstrução é do tipo FIR, que não distorce a fase do sinal.
Escolhendo o trecho da onda reconstruída que está livre dos transitórios decorrentes da filtragem, e calculando a FFT desse trecho, obtém-se o espectro mostrado na Figura 6.
Note que houve uma melhora do nível de ruído de quantização, quando comparado com o espectro original. O script a seguir calcula a FFT da senoide reconstruida.
% Gera a quantização da senoide ideal
Numero_de_Bits = 8; % Especifica o numero de bits
seno_rec = up(129:513);
%Gera ruido de quantização aleatório
ruido = (rand(length(seno_rec ),1) -0.5) / 2^Numero_de_Bits;
senoq = seno_rec + ruido'; % Gera a senoide com ruido de quantização
Cte = (2^Numero_de_Bits) - 1; % Calcula a potência de 2
seno1_quantizado = round(senoq * Cte); % gera o seno quantizado sem a componente CC
figure(4); % Abre a figura 3
fftseno1_quant = abs(fft(seno1_quantizado)); % Prepara a FFT
plot(20 * log10((fftseno1_quant/max(fftseno1_quant))+ 10^-16)); % Plota a FFT
grid; % Gera a grade
xlabel('Frequencias');
ylabel('Amplitude normalizada em dB');
title('FFT da senoide reconstruida');
%
Downsampling
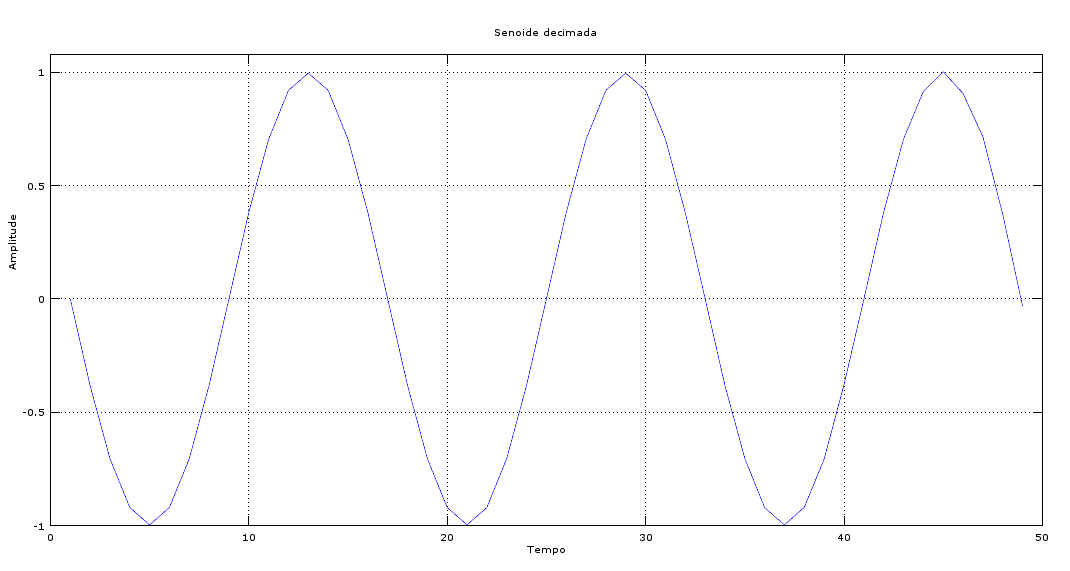
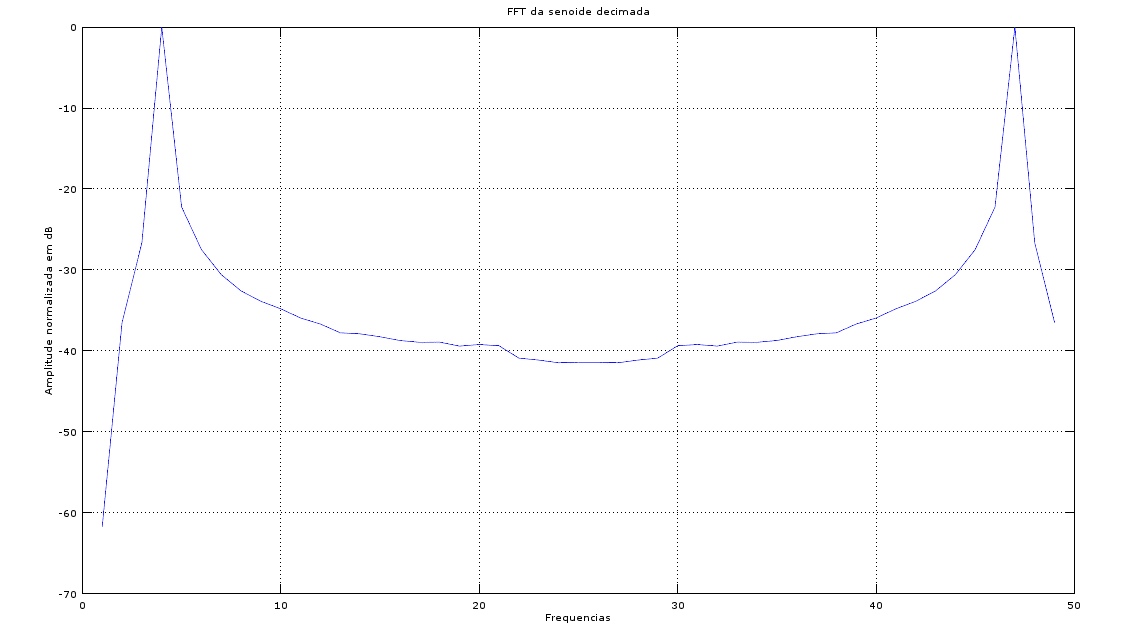
Downsampling ou decimação é a técnica de redução da taxa de amostragem. Isso é feito simplesmente separando uma amostra a cada N. Há uma inevitável distorção do sinal. Na Figura 7 está retratada a forma de onda decimada e na Figura 8 o seu espectro.
O script para gerar a decimação ilustrada nas Figuras 7 e 8 encontra-se a seguir.
% Gera e plota uma senoide ideal amostrada com upsampling
Num_Amostras = 16; % Define o número de amostras por ciclo
Num_Ciclos = 4; % Define o número de ciclos
Delta_t = 1/Num_Amostras; % Define o delta t entre as amostras
tempo = 0:Delta_t:Num_Ciclos - Delta_t; % Define os tempos para gerar a senoide
seno1 = 0.5 * (1 + sin(2 * pi * tempo)); % gera a senoide
close all; % Fecha todas as figuras
figure(1); % Abre a figura 1
plot(seno1); % Plota o seno na figura 1
hold; % Retém a figura
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
title('Senoide ideal amostrada');
plot(seno1, 'x'); % Marca os pontos amostrados
seno1 = seno1 - 0.5; % Suprime a componente CC
figure(2); % Abre a figura 2
%Upsampling
fator_up = 8; % Define fator de upsampling
y = upsample(seno1,fator_up);
plot(y);
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
title('Upsampling da senoide ideal amostrada');
%
% gera filtro fir passa-baixas
lp_fir = fir1(128, 0.2);
up = conv(y,lp_fir) * Num_Amostras ; % Calcula a convolução dos sinais
seno_dec = decimate(up(129:513),8); % Realiza a decimação
figure(3); % Abre a figura 3
plot(seno_dec);
grid; % Gera a grade
xlabel('Tempo');
ylabel('Amplitude');
title('Senoide decimada');
%
% Gera a quantização da senoide decimada
Numero_de_Bits = 8; % Especifica o numero de bits
%Gera ruido de quantização aleatório
ruido = (rand(length(seno_dec ),1) -0.5) / 2^Numero_de_Bits;
senoq = seno_dec + ruido'; % Gera a senoide com ruido de quantização
Cte = (2^Numero_de_Bits) - 1; % Calcula a potência de 2
seno1_quantizado = round(senoq * Cte); % gera o seno quantizado sem a componente CC
figure(4); % Abre a figura 3
fftseno1_quant = abs(fft(seno1_quantizado)); % Prepara a FFT
plot(20 * log10((fftseno1_quant/max(fftseno1_quant))+ 10^-16)); % Plota a FFT
grid; % Gera a grade
xlabel('Frequencias');
ylabel('Amplitude normalizada em dB');
title('FFT da senoide decimada');
%
Conclusão
As técnicas apresentadas neste artigo técnico são muito úteis para a manipulação de sinais digitalizados. São aplicadas para se desenvolver sistemas de controle ou filtragens adaptativas. É necessário relembrar que, como quase tudo na vida real, essas técnicas têm limitações que devem ser consideradas, e que não existem soluções perfeitas. As soluções são sempre de compromisso. Assim cabe ao projetista escolher, segundo os seus critérios, a melhor solução para o seu projeto.
Referências
[1] Processamento Digital de Sinais – DSP – Parte 2 [2] Enhancing ADC resolution by oversamplingCrédito para a imagem destacada: Roundness – Van Truan | Dreamstime Stock Photos